Нормальная форма Хомского

Определение 8.3.1. Грамматика в нормальной форме Хомского (грамматика в бинарной нормальной форме, квадратичная грамматика, grammar in Chomsky normal form) - контекстно-свободная грамматика 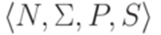, в которой каждое правило имеет один из следующих трех видов: , , 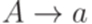, 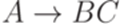где , , , .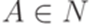

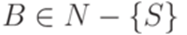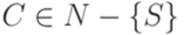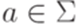Пример 8.3.2. Грамматика

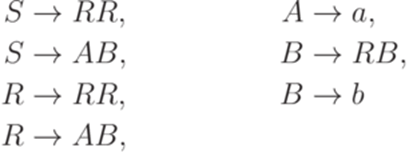
является грамматикой в нормальной форме Хомского.

Теорема 8.3.3. Каждая контекстно-свободная грамматика эквивалентна некоторой грамматике в нормальной форме Хомского.

Доказательство. Пусть дана контекстно-свободная грамматика . Проведем ряд преобразований этой грамматики так, что порождаемый ею язык остается неизменным.

Если правая часть какого-нибудь правила содержит символ S, то заменим грамматику 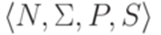на грамматику

где S₀ - новый символ, не принадлежащий множеству .

Заменим во всех правилах каждый терминальный символ a на новый нетерминальный символ T_a и добавим к множеству P правила 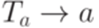для всех .

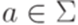Устраним правила вида 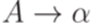, где 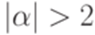, заменив каждое из них на ряд более коротких правил (при этом добавляются новые нетерминальные символы).

Теперь устраним все правила вида 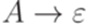, где A не является начальным символом. Это можно сделать так же, как в доказательстве теоремы 8.2.1.

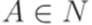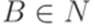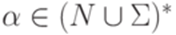Если для каких-то , и множество P содержит правила 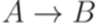и 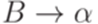, но не содержит правила , то добавим это правило в P. Повторяем эту процедуру, пока возможно. После этого исключим из множества P все правила вида .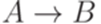

Пример 8.3.4. Грамматика

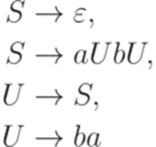
эквивалентна следующей грамматике в нормальной форме Хомского:

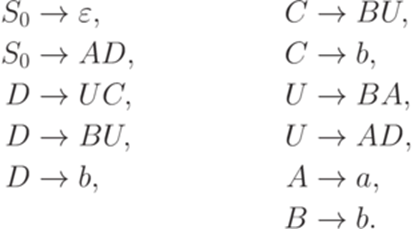
Теорема 8.3.5. Если контекстно-свободный язык не содержит пустого слова, то он порождается некоторой грамматикой, в которой каждое правило имеет один из следующих двух видов: 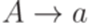, , 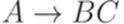где , , , .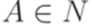

 

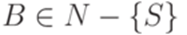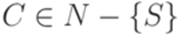8.4*. Нормальная форма Грейбах

Определение 8.4.1. Грамматика в нормальной форме Грейбах (grammar in Greibach normal form) - контекстно-свободная грамматика 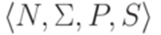, в которой каждое правило имеет один из следующих четырех видов: 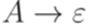, , 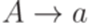, , 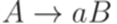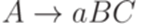где , , , .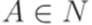

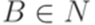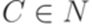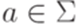Пример 8.4.2. Грамматика

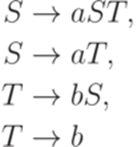
является грамматикой в нормальной форме Грейбах.

Замечание 8.4.3. Некоторые авторы разрешают в грамматиках в нормальной форме Грейбах использовать также правила вида 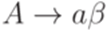, где 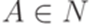, , 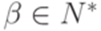(в определении 8.4.1 разрешены, только если ).

Теорема 8.4.4. Каждая контекстно-свободная грамматика эквивалентна некоторой грамматике в нормальной форме Грейбах.

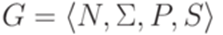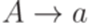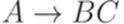Доказательство. Докажем теорему для контекстно-свободных языков, не содержащих пустого слова. Согласно теореме 8.3.5 исходный язык порождается некоторой грамматикой , в которой каждое правило имеет вид или , где , , , .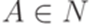

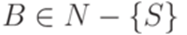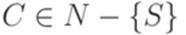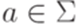Введем |N|² новых вспомогательных символов, соответствующих упорядоченным парам из множества . Новый символ, соответствующий паре 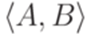, будем обозначать (A\B). Построим грамматику "почти в нормальной форме Грейбах" 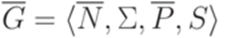, положив 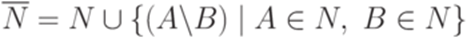и

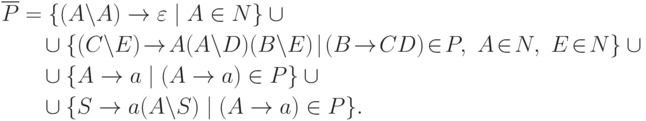
Если в этой грамматике заменить

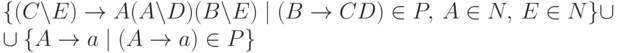
на

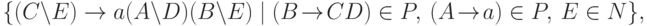
получим эквивалентную ей грамматику в нормальной форме Грейбах. Осталось лишь доказать, что .

Сначала проверим индукцией по длине слова 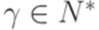, что если 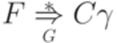, то 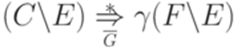для любого 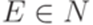. Чтобы провести шаг индукции, допустим, что и

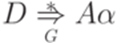где и 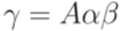. По предположению индукции имеем 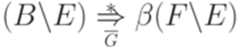и 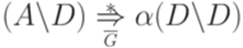. Подключая эти выводы к правилу и используя 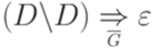, получаем искомый вывод .

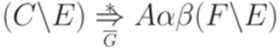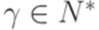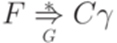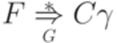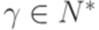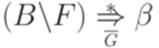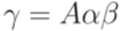Докажем теперь, что для любого равносильны утверждения и . В одну сторону это следует из только что доказанного. Доказательство того, что если , то , проведем индукцией по длине слова . Чтобы провести шаг индукции, допустим, что , , , и . По предположению индукци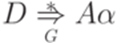и и . Получаем искомый вывод

 

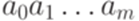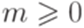Теперь убедимся, что . Рассмотрим произвольное слово , где и 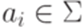для всех 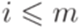. Пусть

где 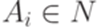для всех 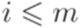. Тогда

Обратно, пусть

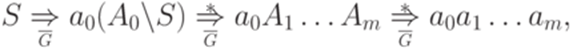
где 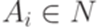для всех 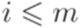. Тогда

Пример 8.4.5. Грамматика

эквивалентна следующей грамматике в нормальной форме Грейбах:

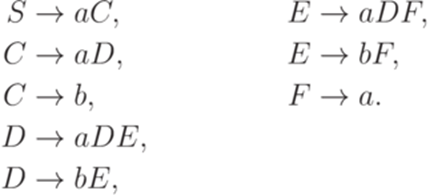
Здесь C, D, E и F соответствуют символам (A\S), (A\T), (V\T) и (U\T) из доказательства теоремы 8.4.4 (удален 21 бесполезный символ).

Теорема 8.4.6. Пусть язык L контекстно-свободный. Тогда язык 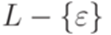порождается некоторой грамматикой в нормальной форме Грейбах без 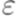- правил.

Пример 8.4.7. Грамматика

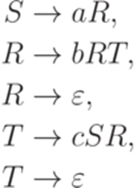
эквивалентна следующей грамматике в нормальной форме Грейбах без 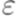-правил:

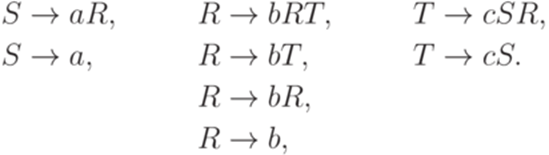
Упражнение 8.4.8. Найти контекстно-свободную грамматику в нормальной форме Грейбах, эквивалентную грамматике

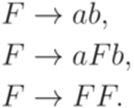
Упражнение 8.4.9. Найти контекстно-свободную грамматику в нормальной форме Грейбах, эквивалентную грамматике

Упражнение 8.4.10. Найти контекстно-свободную грамматику в нормальной форме Грейбах, эквивалентную грамматике

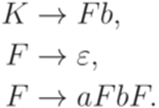
Упражнение 8.4.11. Найти контекстно-свободную грамматику в нормальной форме Грейбах, эквивалентную грамматике

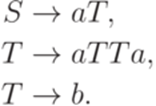
В "лекции 2" были доказаны лемма о разрастании и свойства замкнутости класса автоматных языков. Некоторые из этих теорем имеют аналоги для класса контекстно-свободных языков (разделы 9.1 и 9.4), но этот класс не замкнут относительно дополнения и пересечения (раздел 9.5).

Лемма о разрастании для контекстно-свободных языков формализует явление "периодичности" в этих языках. Для полноты картины в разделах 9.2* и 9.3 приведены некоторые аналогичные теоремы для класса линейных языков, хотя ни в теории, ни в практических приложениях класс линейных языков значительной роли не играет.

В разделе 9.6 доказывается, что пересечение контекстно-свободного языка с автоматным языком является контекстно-свободным. В сочетании с леммой о разрастании этот факт дает удобное средство, позволяющее во многих задачах доказать, что заданный язык не является контекстно-свободным. Еще одно необходимое условие контекстной свободности сформулировано в разделе 9.7*.