Определение 16.1.1. Рассмотрим алфавит  . Пусть
. Пусть  , где
, где  для всех i. Обозначим через
для всех i. Обозначим через  линейную грамматику
линейную грамматику  , где
, где

Обозначим через  язык, порождаемый грамматикой
язык, порождаемый грамматикой  .
.
Лемма 16.1.2. Язык  является непустым тогда и только тогда, когда постовская система соответствия
является непустым тогда и только тогда, когда постовская система соответствия  имеет решение.
имеет решение.
Пример 16.1.3. Рассмотрим постовскую систему соответствия

(то есть n = 2,  и
и  ). Решениями этой системы являются последовательности (1, 1, 2), (1, 1, 2, 1, 1, 2) и т. д. Легко убедиться, что
). Решениями этой системы являются последовательности (1, 1, 2), (1, 1, 2, 1, 1, 2) и т. д. Легко убедиться, что

Теорема 16.1.4. Пусть  . Тогда не существует алгоритма, позволяющего по произвольным контекстно-свободным грамматикам G1 и G2 над алфавитом
. Тогда не существует алгоритма, позволяющего по произвольным контекстно-свободным грамматикам G1 и G2 над алфавитом  узнать, верно ли, что
узнать, верно ли, что  .
.
Доказательство. Сначала докажем утверждение теоремы для случая  . Из леммы 16.1.2 следует, что если бы проблема распознавания свойства
. Из леммы 16.1.2 следует, что если бы проблема распознавания свойства  для контекстно-свободных грамматик над алфавитом
для контекстно-свободных грамматик над алфавитом  была разрешима, то проблема соответствий Поста тоже была бы разрешима. Поэтому из неразрешимости проблемы соответствий Поста следует неразрешимость проблемы распознавания свойства
была разрешима, то проблема соответствий Поста тоже была бы разрешима. Поэтому из неразрешимости проблемы соответствий Поста следует неразрешимость проблемы распознавания свойства  для контекстно-свободных грамматик над алфавитом
для контекстно-свободных грамматик над алфавитом  .
.
Чтобы доказать утверждение теоремы для случая  (например,
(например,  ), достаточно заменить в определении
), достаточно заменить в определении  символ a на ede, символ b на edde и символ c на eddde.
символ a на ede, символ b на edde и символ c на eddde.
Лемма 16.1.5. Язык  является бесконечным тогда и только тогда, когда постовская система соответствия
является бесконечным тогда и только тогда, когда постовская система соответствия  имеет решение.
имеет решение.
Доказательство. Если постовская система соответствия имеет хотя бы одно решение, то она имеет бесконечно много решений.
Теорема 16.1.6. Пусть  . Тогда не существует алгоритма, позволяющего по произвольным контекстно-свободным грамматикам G1 и G2 над алфавитом
. Тогда не существует алгоритма, позволяющего по произвольным контекстно-свободным грамматикам G1 и G2 над алфавитом  узнать, является ли бесконечным язык
узнать, является ли бесконечным язык  .
.
Упражнение 16.1.7. Пусть  . Рассмотрим язык L1, порождаемый грамматикой
. Рассмотрим язык L1, порождаемый грамматикой

и язык L2, порождаемый грамматикой

Верно ли, что  ?
?
Упражнение 16.1.8. Пусть  . Рассмотрим язык L1, порождаемый грамматикой
. Рассмотрим язык L1, порождаемый грамматикой

и язык  , порождаемый грамматикой
, порождаемый грамматикой

Верно ли, что  ?
?
Упражнение 16.1.9. Пусть 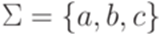 . Рассмотрим язык L1, порождаемый грамматикой
. Рассмотрим язык L1, порождаемый грамматикой

и язык L2, порождаемый грамматикой

Верно ли, что  ?
?
 2020-05-25
2020-05-25 165
165








