Определение 15.1.1. Порождающая грамматика 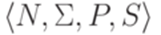 называется неукорачивающей (noncontracting), если для каждого правила
называется неукорачивающей (noncontracting), если для каждого правила 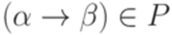 выполняется неравенство
выполняется неравенство 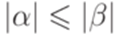 .
.
Теорема 15.1.2. Существует алгоритм, позволяющий по произвольной неукорачивающей грамматике G и по слову wузнать, верно ли, что 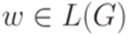 .
.
Теорема 15.1.3. Каждая контекстная грамматика является неукорачивающей. Каждая неукорачивающая грамматика эквивалентна некоторой контекстной грамматике.
Пример 15.1.4. Грамматика
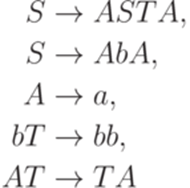
эквивалентна контекстной грамматике из примера 1.5.4.
Упражнение 15.1.5. Найти неукорачивающую грамматику, порождающую язык 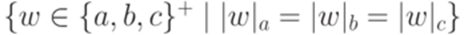 .
.
Упражнение 15.1.6. Найти неукорачивающую грамматику, порождающую язык 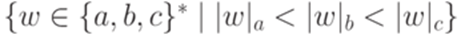 .
.
Упражнение 15.1.7. Найти неукорачивающую грамматику, порождающую язык 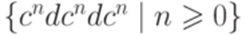 .
.
Упражнение 15.1.7. Найти неукорачивающую грамматику, порождающую язык  .
.
15.2*. Линейно ограниченные автоматы
Определение 15.2.1. Машина Тьюринга
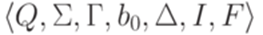
называется линейно ограниченным автоматом (linear bounded automaton), если не существует таких 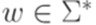 ,
, 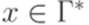 ,
,  ,
, 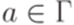 и
и  , что
, что 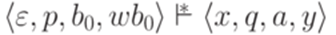 и |xay| > |b0wb0|.
и |xay| > |b0wb0|.
Теорема 15.2.2. Язык L, не содержащий пустого слова, порождается некоторой неукорачивающей грамматикой тогда и только тогда, когда существует линейно ограниченный автомат (в общем случае недетерминированный), допускающий язык L.
Замечание 15.2.3. Неизвестно, верен ли аналог теоремы 15.2.2 для детерминированных линейно ограниченных автоматов.
Теорема 15.2.4. Класс языков, порождаемых неукорачивающими грамматиками, то есть класс контекстных языков, замкнут относительно операций объединения, пересечения и дополнения.
Замкнутость относительно операции дополнения доказали в 1987 году (независимо друг от друга) Нил Иммерман (Neil Immerman) и Роберт Селепчени (Robert Szelepcs) (см. [Imm, Sze]). Замкнутость относительно операции объединения очевидна, а пересечение выражается через объединение и дополнение.
Упражнение 15.2.5. Является ли контекстным язык
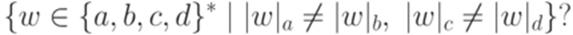
Упражнение 15.2.6. Является ли контекстным язык
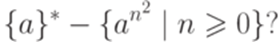
 2020-05-25
2020-05-25 162
162








