Проблема выводимости слова

Теорема 15.3.1. Существует алгоритм, позволяющий по произвольной контекстно-свободной грамматике G узнать, верно ли, что .

Теорема 15.3.2. Существует алгоритм, позволяющий по произвольной контекстно-свободной грамматике G и по слову w узнать, верно ли, что .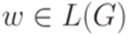

Упражнение 15.3.3. Принадлежит ли слово aaaaabbbabb языку, порождаемому грамматикой

Упражнение 15.3.4. Принадлежит ли слово abababa языку, порождаемому грамматикой

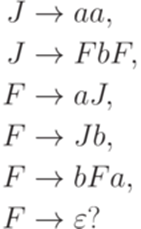
Проблема пустоты языка

Теорема 15.4.1. Существует алгоритм, позволяющий по произвольной контекстно-свободной грамматике G узнать, верно ли, что .

Доказательство. Удалим из G все бесполезные символы, кроме начального символа (как в доказательстве теоремы 8.1.3). Если полученная грамматика содержит хотя бы одно правило, то .

Упражнение 15.4.2. Является ли непустым язык, порождаемый грамматикой

Проблема бесконечности языка

Теорема 15.5.1. Существует алгоритм, позволяющий по произвольной контекстно-свободной грамматике G узнать, является ли бесконечным язык L(G).

Пример 15.5.2. Рассмотрим контекстно-свободную грамматику G из примера 8.1.4. Чтобы выяснить, является ли язык L(G) бесконечным, удалим сначала все бесполезные символы. Затем устраним все -правила. Так как и , то можно всюду заменить W на Z. Получится грамматика

эквивалентная исходной грамматике G. Очевидно, что эта грамматика не содержит "рекурсивных" нетерминальных символов. Следовательно, язык L(G) является конечным.

Упражнение 15.5.3. Является ли бесконечным язык, порождаемый грамматикой