Основные свойства электромагнитных волн. Волновое уравнение

Электромагнитной волной (ЭМВ) называется процесс распространения в пространстве с конечной скоростью неразрывно связанных друг с другом переменных электрического и магнитного полей.

Существование ЭМВ вытекает из теории Максвелла, в основе которой лежат два постулата: 1) переменное магнитное поле порождает в окружающем пространстве вихревое электрическое поле (явление электромагнитной индукции); 2) переменное электрическое поле, в свою очередь, порождает в окружающем пространстве вихревое магнитное поле.

За счет непрерывного взаимопревращения электромагнитное поле распространяется в пространстве в виде электромагнитных волн.

Теория Максвелла не только предсказала возможность существования электромагнитных волн, но и установила их основные свойства [4].

1. В электромагнитной волне (ЭМВ) вектора напряженности электрического поля и магнитной индукции совершают колебания в одинаковой фазе:

. (2.77)

Кроме того, вектора напряженности электрического поля 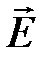и магнитной индукции совершают колебания (рис. 2.21) в плоскости, перпендикулярной скорости распространения волны: , . Следовательно, ЭМВ – поперечная волна [4]. Как видно из рис. 2.21, на котором изображена «моментальная фотография ЭМВ», вектора , и образуют правую тройку.

Рис. 2.21

Уравнения (2.77) являются решениями волновых уравнений ЭМВ [4]:

(2.78)

В левой части волновых уравнений (2.78) использовано обозначение оператора Лапласа:

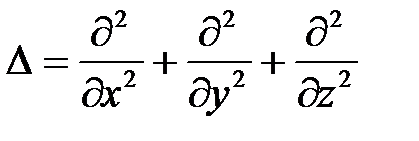. (2.79)

2. Электромагнитные волны могут распространяться как в веществе, так и в вакууме. Скорость распространения ЭМВ в среде зависит от электрических и магнитных свойств вещества.

Скорость с распространения ЭМВ в вакууме является максимальной и выражается через электрическую (e₀) и магнитную (m₀) постоянные:

. (2.80)

В любой среде электромагнитные волны распространяются со скоростью , меньшей, чем в вакууме:

, (2.81)

где – абсолютный показатель преломления данного вещества, зависящий от относительной диэлектрической e и относительной магнитной проницаемости m среды [4]. Таким образом, скорость ЭМВ в веществе равна

. (2.82)

3. Если электромагнитная волна попадает на границу раздела двух сред с различными абсолютными показателями преломления n ₁ и n ₂, то происходит отражение и преломление ЭМВ (рис. 2.22). При этом выполняются следующие законы [4]:

- падающий, отраженный и преломленный лучи, а также перпендикуляр к границе раздела сред, восстановленный в точке падения луча, лежат в одной плоскости (рис. 2.22);

- закон отражения: ;

- закон преломления:

, (2.83)

где n ₂₁ – относительный показатель преломления второй среды относительно первой.

Рис. 2.22

Кроме того, при переходе ЭМВ из одной среды в другую, период Т волны и ее частота ν остаются неизменными, а скорость u и длина волны λ изменяются, так как

, (2.84)

где l – длина волны в вакууме, l_ср – длина волны в среде.

Рассматривая отражение электромагнитной волны от границы раздела двух сред, необходимо учитывать соотношение между показателями преломлений этих двух сред. Так, если ЭМВ отражается от оптически более плотной среды (), то фаза колебаний вектора изменяется на (вектора и направлены в противоположные стороны, рис. 2.23, а). При этом фаза вектора не изменяется (вектора и сонаправлены, рис. 2.23, а) [3]. При отражении ЭМВ от оптически менее плотной среды (), наоборот, изменяется скачком на фаза колебаний вектора магнитной индукции, при этом фаза колебаний вектора остается прежней (рис. 2.23, б).

Рис. 2.23

Изменение на фазы векторов или , означает что при отражении падающей на границу раздела двух сред плоской ЭМВ, тройка векторов , и 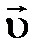поворачивается на угол 180^° либо вокруг вектора (если , рис. 2.23, а), либо вокруг вектора (если , рис. 2.23, б) [3].

4. Электромагнитные волны материальны. Распространяясь в пространстве, они обладают массой, импульсом, производят давление на поверхность, на которую они падают [4].

5. В любой момент времени объемные плотности энергии электрического () и магнитного () полей электромагнитной волны одинаковы: