Оптическая длина пути и оптическая разность хода. Условия максимума и минимума интенсивности света

Скорость света зависит от того в какой среде он распространяется, поэтому за одно и то же время, в разных средах свет будет проходить неодинаковые расстояния.

Оптической длиной пути L световой волны называется произведение расстояния S, пройденного волной в данной однородной среде, на абсолютный показатель преломления этой среды:

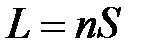Оптическая разность хода двух когерентных волн – разность их оптических путей:

Оптическая разность хода – величина алгебраическая: она может быть положительной или отрицательной [5].

Рассмотрим интерференцию двух световых волн, распространяющихся в разных средах от когерентных источников 1 и 2, с одинаковой начальной фазой (cм. рис. 3.4). Тогда уравнения этих световых волн могут быть записаны в виде:

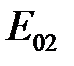где и – амплитуды интерферирующих волн.

Рис. 3.4

Квадрат результирующей амплитуды при сложении колебаний, направленных вдоль одной прямой, определяется выражением

где 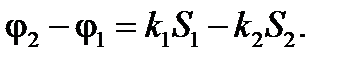,а так как и , то

, (3.2)

где – длина световой волны в среде с показателем преломления n, а l– длина этой же волны в вакууме.

Из выражения (3.1) следует, что интерферирующие волны 1 и 2 будут максимально усиливать друг друга в случае, когда , т. е. разность фаз волн 1 и 2 должна быть равна , где – целое число. Следовательно, с учетом формулы (3.2) получаем, что при максимальном усилении волн: или

Оптическая разность хода равна четному числу полуволн – условие максимума интенсивности.

Также из выражения (3.1) получаем, что интерферирующие световые волны наиболее ослабляют друг друга при , т. е. когда их разность фаз равна . Следовательно, при максимальном ослаблении волн: или