Электропроводность и закон Ома

На электрон в электрическом поле  и магнитном поле  действует сила , равная , поэтому уравнение движения электрона имеет вид

.                     (2.40)

В отсутствие столкновений внешнее электрическое поле однородно смещает все точки сферы Ферми в к-пространстве (рис.). Под действием постоянной силы , действующей в течение промежутка времени , каждый электрон с волновым вектором  получает приращение . Это эквивалентно смещению сферы Ферми, как целого, на расстояние . Теперь полный импульс равен (до включения поля суммарный импульс электронов был равен нулю). Включение постоянного внешнего поля увеличивает энергию системы на величину .

Интегрируя (2.40) при = 0, получим:

.                               (2.41)

Если поле  включено в момент времени , то электроны, заполнявшие сферу Ферми так, что ее центр находился в начале координат к-пространства, спустя время  окажутся в других точках к-пространства; центр сферы окажется смещенным из начала координат на расстояние , причем

.                                    (2.42)

Вследствие столкновений электронов с примесями, дефектами решетки или фононами сфера Ферми может стационарно сохранить свое смещенное положение при заданном электрическом поле. Распределение не меняется – сфера остается сферой. Если среднее время между столкновениями равно , то стационарное в данном поле смещение сферы Ферми равно: .

Для приращения скорости   имеем:

.                                      (2.43)

Если в единице объема мы имеем 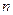 электронов, каждый с зарядом , то в постоянном электрическом поле  плотность тока, вызванного полем , равна

.                                (2.44)

Это выражение имеет форму закона Ома: ; следовательно, из (2.44) имеем для :

.                                      (2.45)

Удельное сопротивление  есть величина, обратная электропроводности, т.е.

.                                         (2.46)

Электропроводность можно интерпретировать так. Смещенный заряд ~ плотности заряда ; множитель  появляется потому, что ускорение заряда в данном поле  ~ заряду электрона и обратно пропорционально массе, а потому  характеризует время, в течение которого поле действует на свободный носитель. Каждое последующее столкновение полностью «стирает» у электрона память о предыдущих, формируя среднюю дрейфовую скорость. Можно изготовить столь чистый кристалл меди, что его проводимость при температуре жидкого гелия будет почти раз больше, чем при комнатной температуре. В последнем случае время релаксации  с. Можно также ввести среднюю длину свободного пробега электронов проводимости, определив ее соотношением

,                                      (2.47)

где - скорость электронов на поверхности Ферми.

Отметим, что столкновения претерпевают лишь те электроны, которые в к-пространстве лежат вблизи поверхности Ферми. Так как для меди , то (300 К) ; (4 К) . При температуре жидкого гелия у ряда очень чистых металлов наблюдалась средняя длина свободного пробега ~ 10 см.