Дискретизация области на совокупность конечных элементов

Разбиение области на подобласти – конечные элементы (КЭ) представляет собой первый шаг на пути к решению задачи. Этот шаг не имеет теоретического обоснования. Искусство разбиения области на конечные элементы зависит от имеющихся навыков исследователя. Плохое разбиение будет приводить к ошибочным результатам, если даже остальные этапы МКЭ осуществляются достаточно точно.

Дискретизация области (тела) включает задание числа, размеров и формы подобластей (КЭ), которые используются для построения дискретной модели реального тела. Это очень деликатная ситуация. С одной стороны, элементы должны быть выбраны достаточно малыми, чтобы получились приемлемые результаты, а с другой стороны, применение достаточно крупных элементов сокращает вычислительную работу. В области больших величин градиентов размеры элементов уменьшаются.

Используются элементы различных типов: а) одномерный элемент (схематически он отрезок, хотя может иметь поперечное сечение); б) двухмерные элементы (треугольники, четырехугольники); в) трехмерные элементы (тетраэдры, параллелепипеды):

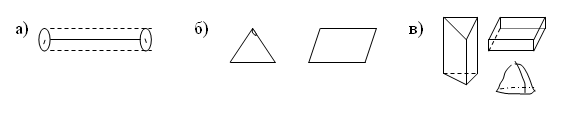
Процесс дискретизации может быть разделен на два этапа: а) разбиение тела на КЭ; б) нумерацию элементов и узлов.

а) Двумерные тела W обычно разбиваются на треугольные или четырехугольные элементы 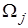. Треугольные элементы – простейшие из двумерных элементов в смысле аналитической формулировки задачи и, видимо, это наилучший способ разбиения. При разбиении двумерной области сначала тело делится на треугольные и четырехугольные подобласти. Границы между подобластями должны проходить там, где изменяются геометрия, приложенная нагрузка или свойства материала. Например, разбиение четырехугольника с помощью короткой диагонали предпочтительнее, потому что элементы, близкие по форме к равностороннему треугольнику, приводят к более точным результатам, чем длинные и узкие треугольники.

Пример:

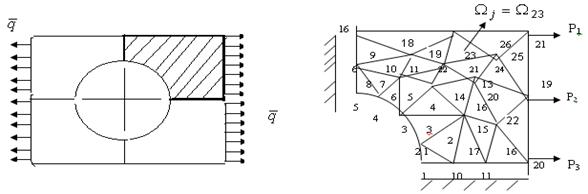
Рис.8.1 Пластина с отверстием. Рис.8.2 Разбиение на треугольные КЭ.

б) В МКЭ решение задачи в конечном счете сводится к решению системы линейных алгебраических уравнений обычно с ленточной матрицей. Ширина полосы матрицы связана с требуемым объемом памяти ЭВМ и вычислений (уменьшение сокращает объем вычислений). Минимизация ширины полосы матрицы связана с минимизацией максимальной по элементам величины наибольшей разности между номерами узлов в отдельных элементах.

Ширина полосы 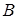 определяется по формул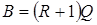е: , где 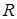 – максимальная по элементам величина наибольшей разности между номерами узлов в отдельном элементе,  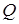– число неизвестных (число степеней свободы) в каждом узле. Минимизация величины  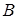связана с минимизацией 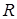. Поэтому, в частности, выгодна последовательная нумерация узлов при движении в направлении наименьшего размера тела. Нумерация элементов не влияет на вычислительные аспекты задачи.