Определение аппроксимирующих ( координатных) функций

для отдельных КЭ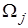

Согласно методу КЭ искомая непрерывная функция  аппроксимируется дискретной моделью, которая строится на множестве кусочно непрерывных функций, определенных на конечном числе подобластей (КЭ). Таким образом, вводятся функции:

            ,                                (8.25)

где k – число КЭ, N - число узлов расчетной схемы КЭ. Тогда искомая функция для всей области :   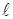- общее число степеней свободы,  степени свободы 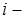го узла. 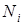-число узлов 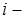го КЭ.

В качестве аппроксимирующих функций КЭ чаще всего применяются полиномы.

Например, для одномерного симплекс – элемента (КЭ) и двумерного симплекса (КЭ)

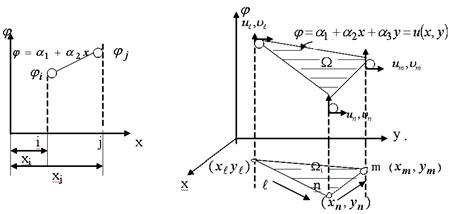
Рис. 8.3 Одномерный КЭ            Рис.8.4 Двумерный КЭ

Можно использовать аппроксимирующие полиномы более высокого порядка (нелинейные). Далее значения искомой функции  в любой точке внутри элемента можно выразить через координаты этой точки и значения функции в узлах элемента.

Пусть  =  или                   (8.26)

,                                                            (8.26.1)

,                                                            (8.26.2)

,                                                             (8.26.3)

В узлах КЭ выполняются следующие условия:

или 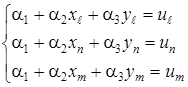                             (8.27)

или в матричной форме

.                                                           (8.27¢)

После определения коэффициентов  из системы (8.27) и подстановки их в равенство (8.26.1) получим выражение для :

= ,                  (8.28.1)

где  матрица функции формы го КЭ, 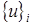- узловые перемещения 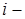го КЭ,

, .                                 (8.29.1)

Остальные коэффициенты 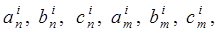 получаются из (8.29.1) с помощью круговой перестановки индексов , т.е.

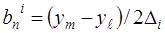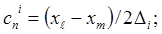,                                    (8.29.2)

,   

, .                               (8.29.3)

Здесь    площадь го треугольного КЭ,

причем, .

Аналогично определяются  для (8.26.2) го КЭ и определяется выражение для функции :

(8.28.2)

Окончательно в матричной форме:

. . (8.30)

Здесь следует отметить, что выражения (8.28.1) и (8.28.2) для  и 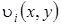 можно было записать в виде:

                                 (8.31)

где , то есть  определены для всей области, но в узлах они равны нулю кроме го KЭ.

3. Получение из отдельных координатных функций элементов
кусочно – непрерывной функции для всей области

При определении координатных функций для КЭ по (8.25) или (8.26) искомая функция для всей области W определяется в виде:

, (8.32)

где 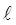- общее число степеней свободы (в общем случае не равно числу узлов, т.е. в каждый узел может быть введено различное число степеней свободы), - степени свободы в МКЭ, которые предоставляют искомые значения функции  и их производных в узлах расчетной схемы. Для функция 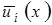 удовлетворяются главные граничные условия. Требования к  следующие: - линейно независимы;  - полная система в энергетическом пространстве оператора А; они удовлетворяют граничным условиям и дифференцируемы. В нашем случае  записываются в виде                                                    (8.33)