2020-05-25
106
минимизации функционала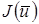 
Условия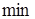 
функционалов (8.2¢) или (8.3) дают для определения значений степеней свободы 
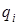соотношения (систему уравнений):
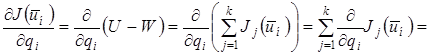
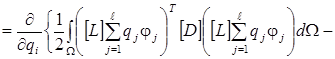
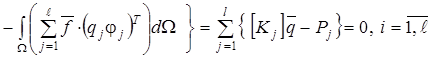или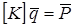 
, (8.34)
где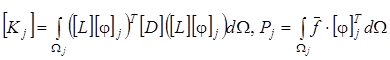 
.
Таким образом, МКЭ дает возможность строить разрешающую систему (8.34)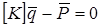 
на основе рассмотрения каждого КЭ. Любая матрица 
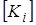является квадратной. Каждая строка матрицы жесткости 
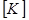соответствует узлу и содержит кроме неизвестных значений 
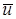в данном узле и неизвестные других узлов КЭ, примыкающих к данному узлу. Матрица 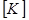имеет размерность (
∙ 
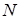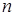)2, где N - число узлов; 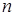- число неизвестных (степеней свободы) в узлах.
Решение полученной разрешающей системы уравнений
Итак, имеется система линейных алгебраических уравнений:
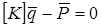. (8.38)
Причем, известные значения неизвестных, которые непосредственно задаются граничными значениями (условиями), могут быть исключены из системы (8.38). Можно поступить и иначе, приняв диагональный элемент матрицы жесткости (соответствующий узлу с известными по граничным условиям неизвестных) равным какой-либо большей величине, намного превышающей значения других элементов.
|
|
|
Полученная система может быть решена методом Гаусса. Но, поскольку она разреженная, то целесообразно применение итерационных методов (Зейделя, последовательной верхней релаксации), Халецкого.
Вычисление искомых величин в элементах
После определения из (8.38) значений неизвестных функций для всех узлов, а далее по ним, зная функции аппроксимации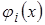 
в КЭ, можно по обычным уравнениям связи определить другие величины, связанные с определяемой величиной. Например, получив значения перемещений с помощью замыкающих соотношений теории упругости (соотношения Коши и закон Гука) можно определить распределения напряжений и деформаций.
