2020-05-25
130
Как видно из только что полученной связи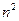 
с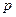 
зависимость показателя преломления 
от частоты волны 
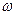определяется отношением 
.
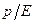Здесь надо сделать две оговорки. Во-первых, поле, действующее на отдельную молекулу (локальное поле), вообще говоря, не совпадает с величиной среднего (макроскопического) поля в среде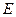 
. Мы не будем учитывать в элементарной теории дисперсии это различие, таким образом, количественные выводы такой теории могут быть применены только к разреженным газам.
Во-вторых, дипольный момент молекулы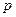 
, наведенный полем световой волны 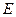, является функцией от времени, т.е. 
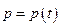. Так как 
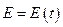и фаза колебаний 
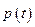не совпадает, в общем случае, с фазой колебаний 
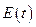, то для нахождения показателя преломления надо усреднить по времени отношение 
.
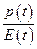Тогда формула для 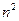приобретет следующий вид:
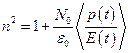(13)
Подставляя выражение для амплитуды A -колебаний электрона, получим: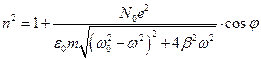 
(14)
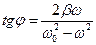(15)
Как показывает опыт, затухание оказывает незначительное влияние на движение оптического электрона, если частота световой волны не равна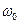 
- собственной частоте колебаний электрона. Точнее, затуханием можно пренебречь, если
|
|
|
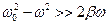(16)
При выполнении этого условия
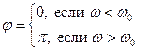(17)
В первом случае (если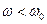 
) колебания электрона происходят в фазе с вынуждающей силой, 
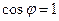. Во втором (
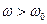) - в противофазе, 
.
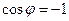Учитывая это можно записать упрощенное выражение для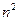 
, применимое для частот далеких от :
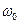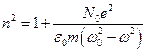(18).
Здесь знак второго слагаемого при 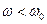положителен, при 
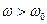второе слагаемое отрицательное.
Для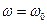 
, 
, 
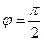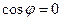, тогда, возвращаясь к исходному выражению для 
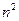, получим: 
.
Проведенный анализ позволяет изобразить примерный вид графика зависимости показателя преломления от циклической частоты, который представлен на рис.5.
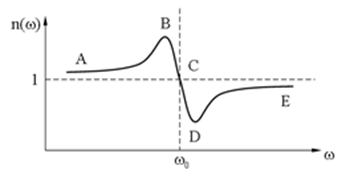
Рис. 5. График зависимости n(ω)
На участках AB и DE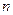 
растет с ростом 
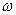- дисперсия нормальная. На участке BCD дисперсия аномальная - с ростом показатель преломления падает.
График 
представлен на рис. 6.
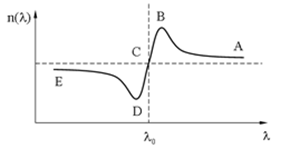
Рис.6. График зависимости n(λ)
