При разработке программы выборочного наблюдения одним из наиболее сложных является вопрос о том, сколько единиц изучаемой совокупности необходимо исследовать, т. е. об объёме выборки.
При этом следует иметь в виду, что при любом способе отбора предельная ошибка выборки обратно пропорциональна числу обследованных единиц. Так как средняя ошибка выборки 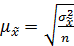 пропорциональна
пропорциональна 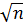 , то при увеличении численности выборки в 4 раза, ошибка уменьшится вдвое. Увеличивая n, можно свести ошибку к min. При n ® N,
, то при увеличении численности выборки в 4 раза, ошибка уменьшится вдвое. Увеличивая n, можно свести ошибку к min. При n ® N, 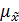 ®0.
®0.
Повышение процента выборки ведёт к увеличению объёма исследуемой работы. В то же время, если в выборку взять недостаточное количество проб, то результаты исследования будут содержать большие погрешности. Всё это необходимо учитывать при организации выборочного обследования.
Формула предельной ошибки выборки используется не только для оценки пределов, в которых находится изучаемый признак в генеральной совокупности, но и для определения необходимого объёма выборки при заданной её ошибке. Для простой случайной повторной выборки имеем:
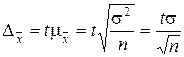 ,
,
откуда получаем: 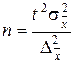 .
.
При проектировании выборочного наблюдения заранее задаётся величина допустимой ошибки 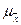 и доверительная вероятность для определения предельной ошибки
и доверительная вероятность для определения предельной ошибки 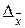 .
.
Если P =0,954, то 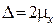 (2σ).
(2σ).
Если P =0,997, то 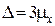 (3σ).
(3σ).
Наибольшую сложность представляет определение величины дисперсии генеральной совокупности. Для определения дисперсии признака в генеральной совокупности используются приближённые методы:
1). Можно провести несколько пробных исследований и по ним выбирать наибольшее значение дисперсии 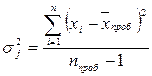 , где достаточно пробных наблюдений.
, где достаточно пробных наблюдений.
2). Можно использовать данные прошлых или аналогичных обследований.
3). Можно использовать размах вариации 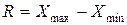 , если распределение нормальное, то
, если распределение нормальное, то 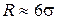 , т. е.
, т. е. 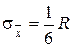 .
.
4). По правилу «трёх сигм», согласно которому в средней величине укладывается примерно три стандартных отклонения (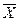 /
/ 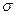 =3; отсюда
=3; отсюда 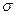 =
= 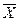 /3).
/3).
Для простой случайной бесповторной выборки расчёт объёма выборки осуществляется по формуле:
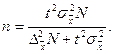
| Объём выборки N | Повторный отбор | Бесповторный отбор |
| При определении среднего размера признака | 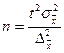 | 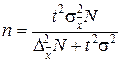 |
| При определении доли признака | 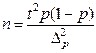 | 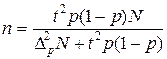 |
Пример 4.
В городе А с целью определения средней продолжительности поездки населения на работу предполагается провести выборочное наблюдение методом случайного повторного отбора. Определить, какой должна быть численность выборки, чтобы с вероятностью 0,954 (и 0,997) ошибка выборочной средней не превышала 5 мин. при среднем квадратическом отклонении 20 мин.
Решение:
1). Численность случайной повторной выборки (P =0,954, t =2):
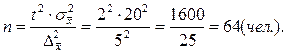
2). Численность случайной повторной выборки (P =0,997, t =3):
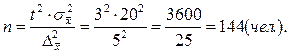
 2020-05-25
2020-05-25 963
963








