Пример построения двойственной задачи и поиска оптимального решения

В качестве исходной задачи – данные задачи об оптимальном ассортименте продукции:

                                        

                                        

                                        

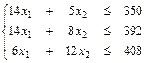
Построим двойственную задачу согласно общим правилам составления двойственных задач.

Так как в прямой задаче в системе ограничений три неравенства, то в двойственной будет три переменные u ₁, u ₂ и u ₃. Так как в исходной задаче две переменные x_j, то число ограничений двойственной задачи будет равно двум (пункт 1).

Ограничения двойственной задачи будут записаны в виде неравенств, противоположного смысла неравенствам системы ограничений прямой задачи (пункт 3).

Учитывая, что целевая функция исходной задачи на max и , то целевая функция двойственной задачи, и система ограничений будут записаны в следующем виде (пункты 4, 5, 6, 7):

                                        

                                        

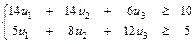
Так как условия системы ограничений прямой задачи являются неравенствами, то соответствующие оценки i -го ресурса – переменные u_i будут положительные (пункт 8):

                               .

Преобразуем задачи (прямую и двойственную) к виду, допускающему применение симплекс-алгоритма. Для этого введем выравнивающие переменные y_j, j =1,…, m в прямую задачу и v_i, i =1,…, n – в двойственную:

1. прямая задача:

          ;

;                         .

 

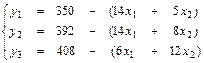2. двойственная задача:

                      ;

                     

или                 

                     

Построим для задач общую симплекс-таблицу, внешний контур которой образует двойственную задачу, внутренний – прямую задачу:

                                                                                               Таблица 1.    

	Б	v1	v2				G
С	С   Б	x1	x2	y1	y2	y3	Коэф. правой части ур-ия (свободн.чл.)	Контрольн. столбец
-u1	y1	14	5	1	0	0	350	370
-u2	y2	14	8	0	1	0	392	415
-u3	y3	6	12	0	0	1	408	427
Коэф. правой части ур-ия (свободн.чл.)	Z	-10	-5	0	0	0	0	-15

В соответствии с алгоритмом симплекс-метода выполняются тождественные преобразования и переходы к новым симплекс-таблицам до тех пор, пока в Z -строке есть отрицательные значения (при Z → max).

                                                                                               Таблица 2.

	Б	u1	v2				G
С	С   Б	x1	x2	y1	y2	y3	Коэф. правой части ур-ия (свободн.чл.)	Контрольн. столбец
- v1	x1	1	0,357	0,071	0	0	25	26,428
-u2	y2	0	3,000	-1,000	1	0	42	45,000
-u3	y3	0	9,857	-0,429	0	1	258	268,428
Коэф. правой части ур-ия (свободн.чл.)	Z	0	-1,43	0,7143	0	0	250	249,28

 

 

                                                                                               Таблица 3.

	Б	u1	u2				G
С	С   Б	x1	x2	y1	y2	y3	Коэф. правой части ур-ия (свободн.чл.)	Контрольн. столбец
- v1	x1	1	0	0,1905	-0,119	0	20	21,07
- v2	x2	0	1	-0,333	0,3333	0	14	15,00
-u3	y3	0	0	2,857	-3,286	1	120	120,571
Коэф. правой части ур-ия (свободн.чл.)	Z	0	0	0,238	0,476	0	270	270,714

 

Таблица 3, в Z -строке которой нет отрицательных чисел – это итоговая таблица, содержащая оптимальное решение.

Оптимальное решение прямой задачи: X =(20,14); Z_max =270.

Оптимальное решение двойственной задачи: U =(0,238;0,470;0); G_min =270.

Значения целевых функций на оптимальных решениях совпадают:

                                      Z_max= G_min

Подставим оптимальный план прямой задачи в систему ограничений:

Первое и второе ограничения прямой задачи выполняются как равенства. Это означает, что ресурсы первого и второго типов полностью используются в оптимальном плане, являются дефицитными и их оценки согласно второй теореме двойственности отличны от нуля (u₁ >0; u₂ >0), дополнительные переменные, соответствующие этим ресурсам равны нулю (y₁ = 0, y₂ = 0 – их нет в базисе оптимального решения).

Третье ограничение выполняется как строгое неравенство, следовательно, ресурс этого типа израсходован не полностью, относится к недефицитным. Остаток этого ресурса в оптимальном плане определяется значением соответствующей дополнительной переменной, входящей в базис оптимальной симплекс-таблицы (y₃ = 120). Следовательно, оценка ресурса: u₃ = 0.

Таким образом, положительную двойственную оценку имеют лишь те типы ресурсов, которые полностью используются в оптимальном плане.

Выполним подстановку оптимальных двойственных оценок ресурсов в систему ограничений:

 

Оба ограничения двойственной задачи выполняются как равенства. Это означает, что двойственные оценки ресурсов, используемых для реализации единицы продукции обоих видов, равны в точности прибыли. Поэтому продавать эти виды продукции экономически целесообразно, а их реализация предусмотрена оптимальным планом прямой задачи (x₁ >0, x₂ >0).

Таким образом, двойственные оценки связаны с оптимальным планом прямой задачи. Всякое изменение исходных данных прямой задачи оказывает влияние на ее оптимальный план и на систему двойственных оценок. В свою очередь двойственные оценки служат инструментом анализа и принятия правильных решений в условиях меняющейся реальной экономической ситуации.