III.Нормальный закон распределения

Определение: Непрерывная случайная величина X имеет нормальный закон распределения (закон Гаусса), если ее плотность распределения имеет вид:

,

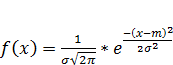Где m=M(X), 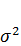=D(X), >0

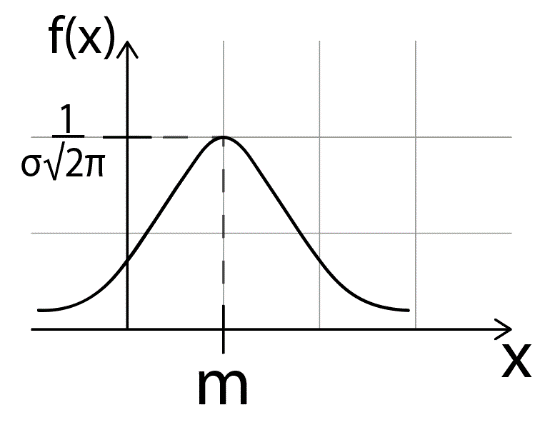Кривую нормального закона распределения называют нормальной или гауссовой кривой

Нормальная кривая

симметрична относительно

прямой x=m, имеет максимум

в т. x=a, равный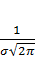

 

Функция распределения случайной величины X, распределенной по нормальному закону, выражается через функцию Лапласа Ф(х) по формуле:

,

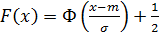Где 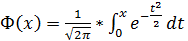 – функция Лапласа.

График функции распределения:

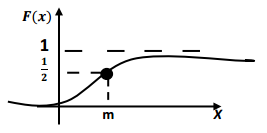
Вероятность того, что случайная величина X примет значения, принадлежащие интервалу (а;b) вычисляются по формуле:

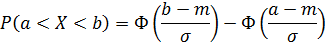
“Правило трех сигм”:Если случайная величина имеет нормальный закон распределения с параметрами mи σ, то практически достоверно, что ее значение заключены в интервале 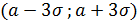, т.к.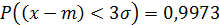

Пример: 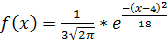. Найти M(x) и D(x).

Решение: M(x)=m=4

D(x)=σ²=9

Пример: Случайная величина xраспределена нормально с математическим ожиданием 32 и дисперсией 16. Найти вероятность того, что в результате испытания xпримет значение из интервала (28;38).

Решение: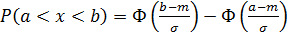

a=28, b=38, m=32, σ=4, получим

 

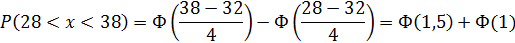
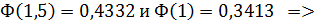
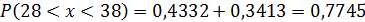
Задачи

1. 30% изделий, выпускаемых данным предприятием, нуждается в дополнительной регулировке. Наудачу отобрано 200 изделий. Найти среднее значение и дисперсию случайной величины X – числа изделий в выборке, нуждающихся в регулировке.

2. Мальчик стреляет в тире до первого попадания. Вероятность попадания в цель при одном выстреле равна 0,01. Составьте закон распределения, найдите функцию распределения и ее график.

3. В партии 10% нестандартных деталей. Наудачу отобраны четыре детали. Написать биномиальный закон распределения дискретной случайной величины X — числа нестандартных деталей среди четырех отобранных. Найти математическое ожидание и дисперсию случайной величины.

4. Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной равна 0,002. Найти вероятность того, что среди 1000 отобранных деталей окажется:

а) 5 бракованных;

б) хотя бы одна бракованная.

5. Случайная величина Х равномерно распределена в интервале (-1;2). Найдите:

а) плотность распределения f(x);

б) функции распределения F(x);

в) числовые характеристики;

г) вероятность Р(4<х<6).

6. Случайная величина Х равномерно распределена в интервале (2;8). Найдите:

а) плотность распределения f(x);

б) функции распределения F(x);

в) числовые характеристики;

г) вероятность Р(3<х<9).

7. Непрерывная случайная величина Х задана плотностью распределения вероятностей:

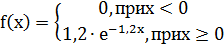
а) Назовите закон распределения рассматриваемой случайной величины.

б) Найдите функцию распределения F(X) и числовые характеристики случайной величины Х.

в) Найдите основные характеристики

8. Непрерывная случайная величина Х задана плотностью распределения вероятностей:

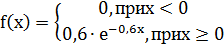
а) Назовите закон распределения рассматриваемой случайной величины.

б) Найдите функцию распределения F(X) и числовые характеристики случайной величины Х.

в) Найдите основные характеристики

9. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины соответственно равны 10 и 4. Найдите:

а) плотность распределения ;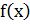

б) вероятность того, что в результате испытания Х примет значение из интервала (8;14).

10. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины соответственно равны 4 и 2. Найдите:

а) плотность распределения ;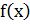

б) вероятность того, что в результате испытания Х примет значение из интервала (3;5).