Определение. Два коллинеарных вектора 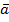 и
и 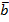 называются противоположно направленными векторами, если их направления противоположны:
называются противоположно направленными векторами, если их направления противоположны:  (рис. 4).
(рис. 4).
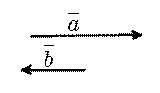
|
| рис. 4 |
Компланарные вектора
Определение. Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами. (рис. 5).

|
| рис. 5 |
Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.
Равные вектора
Определение. Вектора 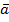 и
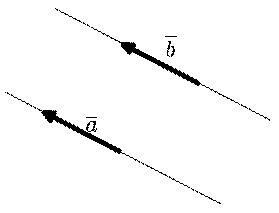
и 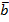 называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны (рис. 6).
называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны (рис. 6).
|
| рис. 6 |
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
Единичный вектор
Определение. Единичным вектором или ортом - называется вектор, длина которого равна единице.
Скалярное произведение
Геометрическая интерпретация. Скалярным произведением двух векторов 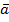 и
и 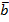 будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:
будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними: 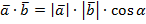
Алгебраическая интерпретация. Скалярным произведением двух векторов 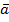 и
и 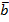 будет скалярная величина, равная сумме попарного произведения координат векторов
будет скалярная величина, равная сумме попарного произведения координат векторов 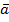 и
и 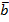 .
.
Формулы скалярного произведения векторов заданных координатами
Формула скалярного произведения векторов для плоских задач
В случае плоской задачи скалярное произведение векторов 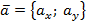 и
и 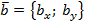 можно найти воспользовавшись следующей формулой:
можно найти воспользовавшись следующей формулой:
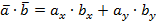
a · b = ax · bx + ay · by
Формула скалярного произведения векторов для пространственных задач
В случае пространственной задачи скалярное произведение векторов 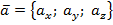 и
и 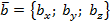 можно найти воспользовавшись следующей формулой:
можно найти воспользовавшись следующей формулой:
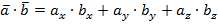
Формула скалярного произведения n -мерных векторов
В случае n-мерного пространства скалярное произведение векторов 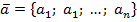 и
и 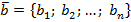 можно найти воспользовавшись следующей формулой:
можно найти воспользовавшись следующей формулой:
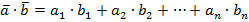
 2020-05-25
2020-05-25 205
205








