Площадь криволинейной трапеции

Пусть функция у = f(x) неотрицательна и непрерывна на отрезке [ a; b ]. График ее изображен на рисунке слева. Поставим задачу определить понятие площади фигуры, ограниченной кривой – графиком функции у = f(x), осью О х, прямыми х = а, х = b, и вычислить площадь этой фигуры, называемой криволинейной трапецией.

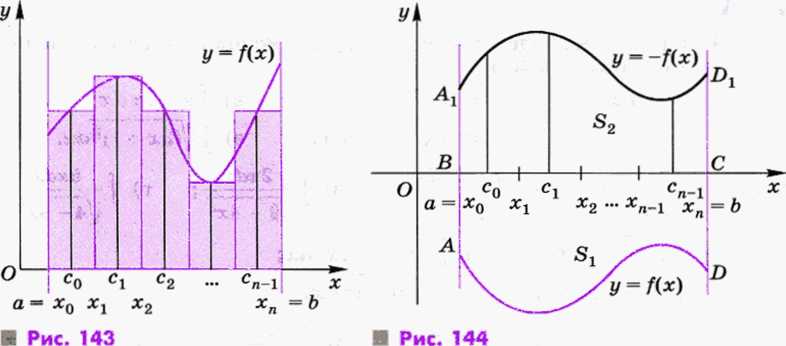
Поставленную задачу естественно решать так. Произведем разбиение отрезка [a; b ] на п частей точками:

а = х₀ < х₁ <... < х_п = b,       (3)

выберем на каждом из частичных отрезков [х_j; х_j+1] (j = 0, 1,......, п – 1) по произвольной точке с_j и составим сумму

S_n = f(c₀) Δ x₀ + f(c₁) Δ x₁ +... + f(c_n) Δ x_n, где

Δ x_j  = x _j+1 – x _j.

Эта сумма, очевидно, равна сумме площадей закрашенных прямоугольников (см. рис. слева).

Устремим теперь все Δ x_j к нулю, неограниченно увеличивая п (п → ), и притом так, чтобы длина самого большого частичного отрезка разбиения стремилась к нулю. Если при этом величина S_n стремится к определенному пределу S, не зависящему от способа разбиения (3) и выбора точек с_} на частичных отрезках, то величину S называют площадью данной криволинейной трапеции. Итак,

S = f(c₀) Δ x₀ + f(c₁) Δ x₁ +... + f(c_n-1) Δ x_n-1).

Пусть теперь функция y = f(x) неположительна и непрерывна на отрезке
[ a; b ] (рис. справа).

Рассмотрим функцию у = – f(x). Она непрерывна и неотрицательна на отрезке [ a; b ]. Криволинейные трапеции A₁BCD₁ и ABCD, ограниченные соответственно кривыми у = – f(x) и у = f(x), а также осью О х и прямыми
х = а и х = b, симметричны относительно оси О х. Поэтому естественно считать, что трапеция ABCD имеет площадь S₁ равную площади S₂ трапеции A₁BCD₁.

Сумму

S_n = f(c₀) Δ x₀ + f(c₁) Δ x₁ +... + f(c_n-1) Δ x_n-1             (4)

называют интегральной суммой.

Таким образом, площадь криволинейной трапеции, расположенной:

а) над отрезком [ a; b ] оси Ох есть предел интегральной суммы S_n, когда maxΔ xj → 0;

б) под отрезком [ a; b ] оси Ох, есть взятый со знаком «минус» предел интегральной суммы S_n,, когда maxΔ xj → 0.

Домашнее задание

Учебник Башмакова, стр. 198-201

Учебник Никольского, 11 класс, §§6.6. 6.7 №6.48, №6.69(а).

Итог урока

Обучающиеся отвечают на вопросы, что они сегодня изучили, что было понятно, а что нет.