Здесь правило еще проще:
- если «точка привязки»  (90
(90  или
или  (270
(270  )
)
– функция меняется на кофункцию;
- если «точка привязки» π (180  ) или 2
) или 2 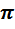 (360
(360  )
)
– функция остается той же.
То есть, при аргументах исходной функции  +
+  ,
,  −
−  ,
,  +
+ 
или 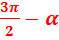 , мы должны поменять функцию, а при аргументах π+
, мы должны поменять функцию, а при аргументах π+  , π−
, π−  , 2π+
, 2π+  или 2π−
или 2π−  - нет
- нет
. Для того, чтоб это легче запомнить, вы можете воспользоваться мнемоническим правилом, которое в школе называют «лошадиным правилом»:
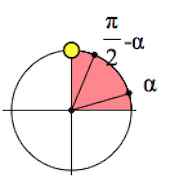
Точки, обозначающие  (90
(90  или
или  (270
(270  )
)
расположены вертикально, и если вы переводите взгляд с одной на другую и назад, вы киваете головой, как бы говоря «да
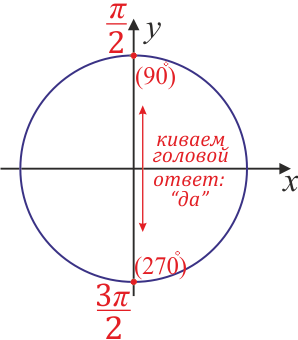
Точки же, обозначающие π (180  ) или 2
) или 2  (360
(360  ) расположены горизонтально, и если вы переводите взгляд между ними, вы мотаете головой, как бы говоря «нет».
) расположены горизонтально, и если вы переводите взгляд между ними, вы мотаете головой, как бы говоря «нет». 
Эти «да» и «нет» - и есть ответ на вопрос: «меняется ли функция?».
Таким образом, согласно правилу, в нашем примере выше cos(3π2−a)=...
косинус будет меняться на синус. В конечном итоге получаем, cos( −
−  )= −sin a
)= −sin a
. Примеры с формулами приведения
Пример:  Преобразуем cos (
Преобразуем cos ( +
+  ).
). 
Наименование функции изменяется на sin  . Далее из того, что 0<
. Далее из того, что 0<  <
<  , следует, что
, следует, что  +
+  — аргумент из второй четверти, а в ней преобразуемая функция косинус имеет знак «минус». Этот знак надо поставить перед полученной функцией. Таким образом, cos (
— аргумент из второй четверти, а в ней преобразуемая функция косинус имеет знак «минус». Этот знак надо поставить перед полученной функцией. Таким образом, cos ( +
+  )= -
)= - 
Пример. Угол 120  лежит во второй четверти,значит в качестве «точки привязки» можем взять либо 180
лежит во второй четверти,значит в качестве «точки привязки» можем взять либо 180  , либо 90
, либо 90 
I способ: 
II способ: 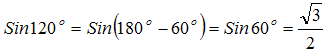
Решение упражнений


Зачем нужны формулы приведения? Ну, например, они позволяют упрощать выражения или находить значения некоторых тригонометрических выражений без использования калькулятора.
Пример. (Задание из ЕГЭ ) Найдите значение выражения 18cos41: sin49∘
Решение:
18cos41  sin49 sin49  = =
|
Углы 41  и 49
и 49  нестандартные, поэтому «в лоб» без калькулятора вычислить непросто. Однако, используя формулы приведения, мы легко найдем правильный ответ.
нестандартные, поэтому «в лоб» без калькулятора вычислить непросто. Однако, используя формулы приведения, мы легко найдем правильный ответ.
Прежде всего, обратите внимание на один важный момент: 49  =90
=90  −41
−41  . Поэтому мы можем заменить на 49
. Поэтому мы можем заменить на 49  на 90
на 90  −41
−41 
| . |
=18cos41  sin(90 sin(90  −41 −41  )= )=
|
Теперь применим к синусу формулу приведения:
|
· – это первая четверть, синус в ней положителен. Значит, знак будет плюс;
- 90
 - находится на «вертикали» - функция меняется на кофункцию.
- находится на «вертикали» - функция меняется на кофункцию.
sin(90  −41 −41  )=cos41 )=cos41 
|
=18cos41  cos41 cos41  = =
|
| =18 |
Ответ: 18
Пример. Вычислите при помощи формул приведения а) sin600  , б) tg480
, б) tg480  , в) cos330
, в) cos330  , г) sin240
, г) sin240 
.Решение: а) sin600  =sin(360
=sin(360  +240
+240  )=
)=  -
-  =−
=− 
б) tg480  =tg(360
=tg(360  +120
+120  )=tg120
)=tg120  =
=  =
= 
в) cos330  =cos(360
=cos(360  −30
−30  )=cos30
)=cos30  =
= 
г) sin24  =sin(270
=sin(270  −30
−30  )=−cos30
)=−cos30  =−
=− 
Задача Упростить выражение:

Решение:
1) 
2) 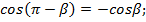
3) 
4) 
5) 
6) 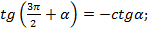
7) 

Ответ: 1.
Вычислить 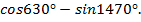
Решение:

1. 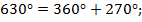

2 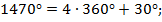

3. 
Ответ: 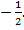
Решить уравнение: 
Решение:






Задача 6. Решите уравнение: 
Решение:
1) 
2) 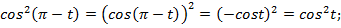
3)  при любом действительном
при любом действительном 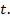
Ответ: 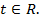
 2020-05-25
2020-05-25 700
700








