Решение логических задач булевой алгебры в программе EXCEL

В настоящее время методы математической логики внедряются в гуманитарные знания как аппарат, позволяющий быстро и эффективно перерабатывать огромные объемы информации. Эти методы, как правило, при объяснении понятий и существующих между ними отношений исключают ошибки, проистекающие за счет неточного толкования смысла понятий, благодаря использованию логических операций.

Впервые с идеей внедрения логики и математики в процесс познания закономерностей между объектами любой природы выступил немецкий философ и математик Лейбниц (1646 – 1716). Он предвидел возникновение новой области науки, названной им философским исчислением.

Философское исчисление, по идее Лейбница, должно представлять такую логическую систему, в которой все производные понятия выражались бы символами, составленными из известных простых символов, обозначающих элементарные понятия на основании строгих правил. Операции над символами должны производиться по аналогии с алгебраическими операциями так, чтобы формальным путем можно было получать все новые и новые понятия и умозаключения.

Грандиозный замысел Лейбница долгое время оставался без развития. Первый крупный шаг в осуществлении идей Лейбница был сделан Джорджем Булем (1815 – 1864). В период с 1847 по 1857 г. он опубликовал три работы. Первые две носили характер предварительных исследований. В третьей работе (это объемистая книга в 424 стр.) изложена, в сущности, вся система Буля. Здесь он демонстрирует, как при помощи символических алгебраических методов можно строить логические конструкции. Кроме того, он показывает, как его система может быть распространена на теорию вероятностей.

В этих работах Буль преследует еще одну цель: найти элементарные операции человеческого мышления, выйдя за рамки дедуктивной и

индуктивной логики. Выражаясь современным языком, его исследования принадлежали к области кибернетики.

Буль впервые показал, что законы человеческого мышления могут быть формализованы так, что над понятиями могут производиться те же операции, что и над целыми числами. Но в отличие от арифметики, как он показал, формальные операции над понятиями подчиняются следующим двум законам: два одних и тех же понятия сложенные или перемноженные приводят к тому же понятию (в современной Булевой алгебре их называют – отсутствие коэффициентов и степеней).

На формирование Булевой алгебры как самостоятельной научной дисциплины оказали влияние исследования немецкого математика Эрнста Шредера (1841–1902), который дал математическую трактовку закона исключенного третьего аристотелевской логики.

Шредер допускал наличие классов больше двух и для оперирования с ними он сформулировал следующее правило: если среди членов некоторой суммы классов находится хотя бы один, который оказывается отрицанием другого, то вся сумма равна единице. Легко показать, что с помощью этого правила можно построить таблицу операции отрицания Булевой алгебры.

Символическое исчисление Буля Шредер называл логическим исчислением и признавал только три основных операции: сложение, умножение и отрицание; вычитание он считал не безусловно выполнимой операцией. Тем самым Шредер поставил вопрос об оптимальном количестве операций в логике классов.

Однако гениальная догадка Буля состояла в том, что только на множестве числа М={0;1} символическое исчисление не противоречит опыту человеческого мышления. Вопрос же об оптимальности количества операций и в логике классов, и в исчислении Буля решается неоднозначно.

Согласно современным представлениям, алгеброй Буля называют элементы множества М={0;1} с заданными в нем операциями S={‘Ú’,’Ù’,’-‘} дизъюнкции, конъюнкции и отрицания. Обозначается алгебра Буля так:

=(М;S), здесь М – множество, S – сигнатура алгебры, т.е. набор операций. Переменные будем называть булевыми переменными. Эти переменные обозначают понятия или высказывания как неделимые понятия, если , то высказывание ложно, если же , высказывание истинно.

Рассмотрим следующие логические задачи, которые решаются на базе символического исчисления Буля.

Задача 1. На уроке по гражданской обороне учитель показывает макет гранаты. Необходимо определить тип этой гранаты и радиус разлета убойных осколков.

Характеристики осколочной гранаты Ф-1

Тип гранаты – Оборонительная Вес гранаты – 600 гр Вес разрывного заряда – 60 гр Тип запала – УЗРГМ Время горения замедлителя – 3,2–4,2 сек Радиус разлета убойных осколков – 200 м Радиус зоны эффективного поражения живой силы – 7 м Средняя дальность броска – 20–40 м

Характеристики осколочной гранаты РГД-5
Тип гранаты: наступательная Вес гранаты – 310 гр Вес разрывного заряда – 60 гр Тип запала УЗРГМ Время горения замедлителя – 3,2–4,2 сек Радиус разлета убойных осколков – 25 м Радиус зоны эффективного поражения живой силы – 5 м Средняя дальность броска – 30–45 м
	Характеристики осколочной гранаты РГО
	Тип гранаты – Оборонительная Вес гранаты – 530 гр Вес разрывного заряда – 92 гр Тип запала – УДЗ Время горения замедлителя – 3,3–4,3 сек Радиус разлета убойных осколков – 150 м Радиус зоны эффективного поражения живой силы – 12 м Средняя дальность броска – 20–40 м

Были получены следующие три ответа.

1. Это наступательная граната с радиусом разлета 150 м.

2. Это оборонительная граната с радиусом разлета убойных осколков 200м.

3. Это не наступательная граната с радиусом разлета осколков 25 м.:

Учитель сказал ребятам, что каждый из них прав только в одном из двух предложений. Какой же тип и радиус разлета убойных осколков представленной гранаты?

С помощью Булевой переменной введем обозначения:

- Это граната наступательная – ;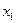

- Радиус разлета осколков равен 150 м.– ;

- Это граната оборонительная – ;

- Радиус разлета осколков равен 200 м. – ;

- Это граната не наступательная – ;

- Радиус разлета осколков равен 24 м. – .

В этих обозначениях ответы кодируются логическими функциями следующим образом:

Ответ 1: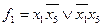

Ответ 2:

Ответ 3:

Кроме того, ясно, что граната может быть только одного типа и иметь определенный радиус разлета убойных осколков. Эти условия позволяют ввести дополнительные логические функции:

Полученные таким образом логические функции представлены в совершенной дизъюнктивной нормальной форме. Если придать всевозможные значения наборам переменных, от которых зависят указанные функции, то можно получить таблицы для .

Пусть все 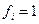, тогда получим систему уравнений булевой алгебры:

(1)

Система (1) представляет математическую модель искомой задачи. Один из способов решения (1) состоит в подборе тех единичных термов логических функций , наборы переменных которых удовлетворяют системе (1), а значения переменных 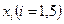из этих наборов не противоречат друг другу.

Для нахождения всех единичных термов системы (1) необходимо произвести вычисление таблиц функций f1, f2, f3, f4, f5. Это можно сделать с помощью программы Microsoft Excel. Для этого:

1. Включите компьютер;

2. После того, как на экране монитора появится рабочий стол операционной системы Windows, откройте окно Microsoft Excel;

3. Заполните ячейки A1¸B4 таблицы, перебрав все варианты значений логических переменных х1 и х5;

4. Постройте таблицу истинности для функции f1, воспользовавшись функциями НЕ, И, ИЛИ, которые находятся в мастере функций 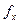в категории ЛОГИЧЕСКИЕ. Для этого:

· активизируйте ячейку С2;

· воспользуйтесь функцией НЕ (см. рис. 1);

· автозаполнением занесите полученные результаты в ячейки С2¸С5 (рис. 2)

Аналогичным способом достроим таблицу истинности для функции f1, используя функции И, ИЛИ. В результате получим значения для х1 и х5, изображённые на рис. 3.