Вероятность произведения независимых событий равна произведению вероятностей этих событий.
Если 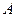 и
и 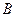 - независимые события, то
- независимые события, то 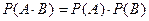 .
.
Эту теорему можно обобщить на любое конечное число независимых событий.
Если 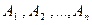 - независимые события, то
- независимые события, то 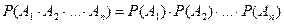 .
.
Задача 3. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором, третьем справочнике соответственно равны 0,6; 0,7; 0,8.
Найти вероятность того, что формула содержится: 1) только в одном справочнике;
2) хотя бы в одном справочнике.
Обозначим элементарные события:
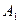 - формула содержится в первом справочнике,
- формула содержится в первом справочнике, 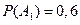
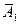 - в первом справочнике формулы нет,
- в первом справочнике формулы нет, 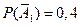
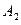 - формула содержится во втором справочнике,
- формула содержится во втором справочнике, 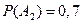
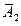 - во втором справочнике формулы нет,
- во втором справочнике формулы нет, 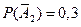
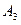 - формула содержится в третьем справочнике,
- формула содержится в третьем справочнике, 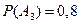
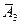 - в третьем справочнике формулы нет,
- в третьем справочнике формулы нет, 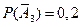 .
.
Событие 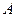 - формула содержится только в одном справочнике
- формула содержится только в одном справочнике
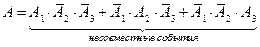 .
.
Применим теоремы о вероятности суммы несовместных событий и вероятности произведения независимых событий:
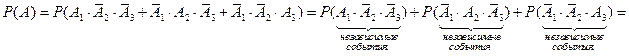
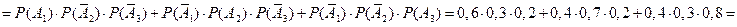
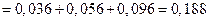 .
.
Событие 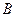 - формула содержится хотя бы в одном справочнике
- формула содержится хотя бы в одном справочнике
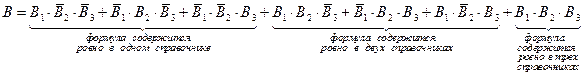 .
.
Событие 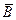 (не
(не 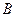 ) - формулы нет ни в одном справочнике,
) - формулы нет ни в одном справочнике, 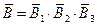 .
.
Противоположные события 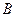 и
и 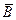 образуют полную группу несовместных событий.
образуют полную группу несовместных событий.
Следовательно, 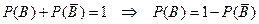 .
.
Применим теорему о вероятности произведения независимых событий:
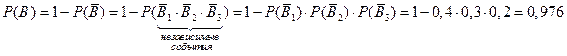 .
.
Задача 4. Трое по очереди бросают монету. Выигрывает тот, у которого первым появится герб.
Какова вероятность выигрыша для каждого игрока?
Обозначим элементарные события:
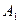 - игрок
- игрок 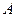 бросает монету 1-ый раз и выигрывает,
бросает монету 1-ый раз и выигрывает, 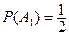
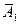 - игрок
- игрок 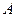 бросает монету 1-ый раз и не выигрывает;
бросает монету 1-ый раз и не выигрывает; 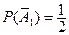
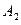 - игрок
- игрок 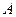 бросает монету 2-ой раз и выигрывает,
бросает монету 2-ой раз и выигрывает, 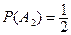
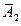 - игрок
- игрок 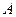 бросает монету 2-ой раз и не выигрывает;
бросает монету 2-ой раз и не выигрывает; 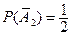
………………………………………………………………………….
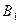 - игрок
- игрок 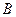 бросает монету 1-ый раз и выигрывает,
бросает монету 1-ый раз и выигрывает, 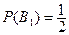
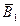 - игрок
- игрок 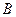 бросает монету 1-ый раз и не выигрывает;
бросает монету 1-ый раз и не выигрывает; 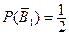
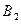 - игрок
- игрок 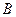 бросает монету 2-ой раз и выигрывает,
бросает монету 2-ой раз и выигрывает, 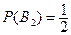
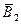 - игрок
- игрок 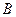 бросает монету 2-ой раз и не выигрывает;
бросает монету 2-ой раз и не выигрывает; 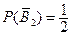
………………………………………………………………………….
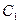 - игрок
- игрок 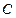 бросает монету 1-ый раз и выигрывает,
бросает монету 1-ый раз и выигрывает, 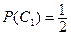
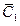 - игрок
- игрок 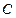 бросает монету 1-ый раз и не выигрывает;
бросает монету 1-ый раз и не выигрывает; 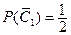
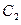 - игрок
- игрок 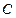 бросает монету 2-ой раз и выигрывает,
бросает монету 2-ой раз и выигрывает, 
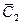 - игрок
- игрок 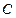 бросает монету 2-ой раз и не выигрывает;
бросает монету 2-ой раз и не выигрывает; 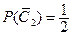
……………………………………………………………………………
Событие 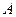 - выиграл первый игрок (
- выиграл первый игрок (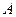 ):
):
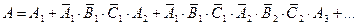
Применим теоремы о вероятности суммы несовместных событий и вероятности произведения независимых событий:
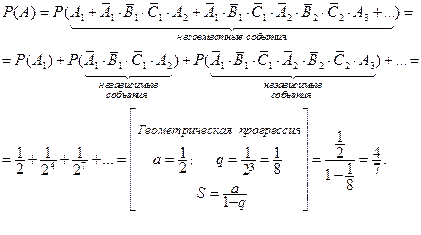
Событие 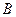 - выиграл первый игрок (
- выиграл первый игрок (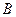 ):
):
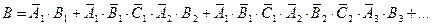
Применим теоремы о вероятности суммы несовместных событий и вероятности произведения независимых событий:
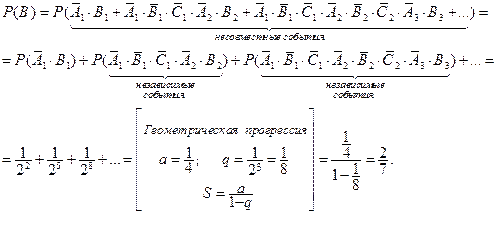
Событие 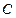 - выиграл первый игрок (
- выиграл первый игрок (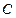 ):
):
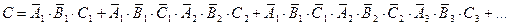
Применим теоремы о вероятности суммы несовместных событий и вероятности произведения независимых событий:
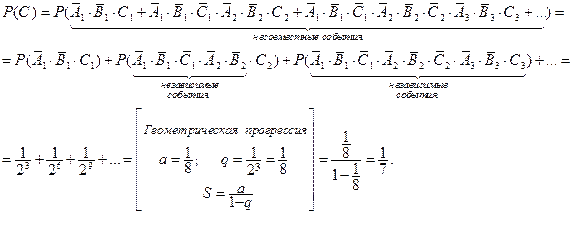
Вероятность события 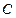 можно найти следующим образом:
можно найти следующим образом: 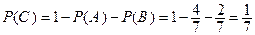 .
.
Задача 5. Игрок 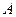 поочередно играет две партии с игроками
поочередно играет две партии с игроками 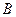 и
и 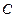 . Вероятности выигрыша в первой партии для
. Вероятности выигрыша в первой партии для 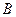 и
и 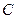 равны соответственно 0,1 и 0,2. Вероятности выиграть во второй партии для игрока
равны соответственно 0,1 и 0,2. Вероятности выиграть во второй партии для игрока 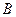 равна 0,3, а для игрока
равна 0,3, а для игрока 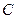 равна 0,4.
равна 0,4.
Определить вероятность того, что 1) первым выиграет 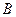 ;
;
2) первым выиграет 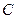 .
.
Обозначим элементарные события:
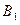 - игрок
- игрок 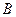 выигрывает в первой партии,
выигрывает в первой партии, 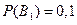
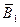 - игрок
- игрок 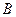 не выигрывает в первой партии,
не выигрывает в первой партии, 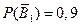
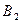 - игрок
- игрок 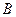 выигрывает во второй партии,
выигрывает во второй партии, 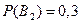
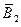 - игрок
- игрок 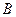 не выигрывает во второй партии,
не выигрывает во второй партии, 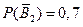
 - игрок
- игрок 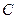 выигрывает в первой партии,
выигрывает в первой партии, 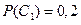
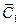 - игрок
- игрок 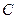 не выигрывает в первой партии,
не выигрывает в первой партии, 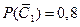
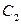 - игрок
- игрок 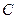 выигрывает во второй партии,
выигрывает во второй партии, 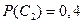
Событие 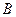 - выигрывает игрок
- выигрывает игрок 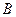 :
:
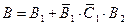
Применим теоремы о вероятности суммы несовместных событий и вероятности произведения независимых событий:
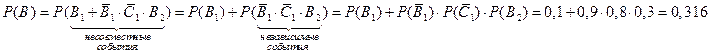 .
.
Событие 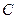 -выиграет игрок
-выиграет игрок 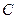 :
:
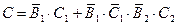
Применим теоремы о вероятности суммы несовместных событий и вероятности произведения независимых событий:
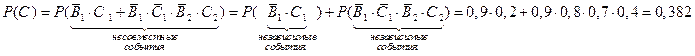 .
.
Задача 6. В двух урнах находятся одинаковые шары, отличающиеся только цветом, причем в первой урне 5 белых, 11 черных, 8 красных шаров, а во второй урне 10 белых, 8 черных, 6 красных шаров. Из обеих урн наудачу извлекают по одному шару.
Какова вероятность того, что оба шара одного цвета?
Обозначим элементарные события:
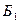 - из первой урны извлекают белый шар,
- из первой урны извлекают белый шар, 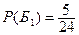
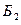 - из второй урны извлекают белый шар,
- из второй урны извлекают белый шар, 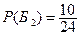
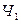 - из первой урны извлекают черный шар,
- из первой урны извлекают черный шар, 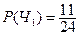
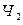 - из второй урны извлекают черный шар,
- из второй урны извлекают черный шар, 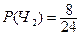
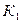 - из первой урны извлекают красный шар,
- из первой урны извлекают красный шар, 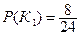
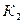 - из первой урны извлекают красный шар,
- из первой урны извлекают красный шар, 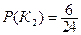 .
.
Событие 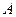 - оба шара одного цвета:
- оба шара одного цвета:
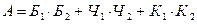 .
.
Применим теоремы о вероятности суммы несовместных событий и вероятности произведения независимых событий:
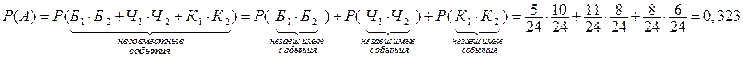
 2020-05-25
2020-05-25 267
267








