Теорема (о вероятности суммы несовместных событий)
Вероятность суммы несовместных событий равна сумме вероятностей этих событий.
Если 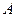 и
и 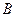 - несовместные события, то
- несовместные события, то 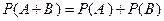 .
.
Следствие 1
Если события 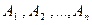 образуют полную группу несовместных событий, то сумма вероятностей этих событий равна единице:
образуют полную группу несовместных событий, то сумма вероятностей этих событий равна единице: 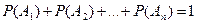 .
.
Следствие 2
Сумма вероятностей противоположных событий равна единице, так как противоположные события 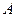 и
и 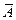 образуют полную группу несовместных событий:
образуют полную группу несовместных событий: 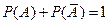 .
.
Задача 2. Для прохождения производственной практики на 30 студентов предоставлено 15 мест на металлургическом заводе, 8 мест на авиационном заводе и 7 мест в университете.
Какова вероятность того, что два определенных студента попадут на практику вместе?
Обозначим элементарные события:
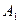 - два определенных студента попадут вместе на металлургический завод;
- два определенных студента попадут вместе на металлургический завод;
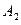 - два определенных студента попадут вместе на практику на авиационный завод;
- два определенных студента попадут вместе на практику на авиационный завод;
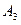 - два определенных студента попадут вместе на практику в университет.
- два определенных студента попадут вместе на практику в университет.
Событие 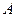 - два определенных студента попадут на практику вместе.
- два определенных студента попадут на практику вместе.
Событие 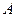 заключается в следующем: два определенных студента попадут вместе на металлургический завод, или (+) два определенных студента попадут вместе на авиационный завод, или (+) два определенных студента попадут вместе в университет:
заключается в следующем: два определенных студента попадут вместе на металлургический завод, или (+) два определенных студента попадут вместе на авиационный завод, или (+) два определенных студента попадут вместе в университет:
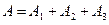 ,
,
где события 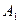 ,
, 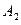 и
и 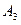 - несовместные, так как не могут произойти одновременно в результате одного опыта.
- несовместные, так как не могут произойти одновременно в результате одного опыта.
Применим теорему о вероятности суммы несовместных событий и получим:
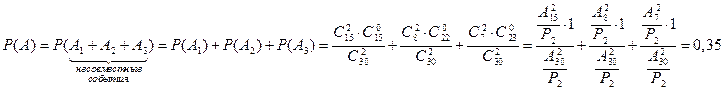
Теорема (о вероятности суммы совместных событий)
Вероятность суммы совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.
Если 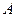 и
и 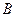 - совместные события, то
- совместные события, то 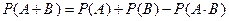 .
.
Вероятность события 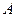 , вычисленная при условии, что событие
, вычисленная при условии, что событие 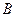 произошло, называется условной вероятностью события
произошло, называется условной вероятностью события 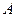 .
.
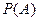 - безусловная вероятность события
- безусловная вероятность события 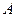 ;
;
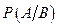 - вероятность события
- вероятность события 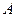 при условии, что событие
при условии, что событие 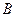 произошло;
произошло;
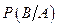 - вероятность события
- вероятность события 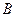 при условии, что событие
при условии, что событие 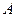 произошло.
произошло.
Событие 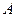 называется независимым от события
называется независимым от события 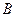 , если вероятность события
, если вероятность события 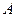 не зависит от того, произошло событие
не зависит от того, произошло событие 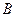 или нет, то есть
или нет, то есть 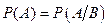 .
.
Независимость событий есть свойство взаимное, то есть если событие 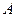 не зависит от события
не зависит от события 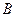 , то и событие
, то и событие 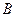 не зависит от события
не зависит от события 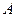 .
.
Событие 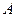 называется зависимым от события
называется зависимым от события 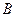 , если вероятность события
, если вероятность события 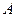 меняется в зависимости от того, произошло событие
меняется в зависимости от того, произошло событие 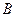 или нет, то есть
или нет, то есть 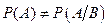 .
.
 2020-05-25
2020-05-25 92
92







