2020-05-25
204
Вероятность произведения зависимых событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло.
Если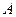 
и 
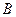- зависимые события, то 
.
Задача 7. Студент знает 20 из 25 вопросов программы.
Найти вероятность того, что студент знает предложенные ему три вопроса.
Событие 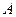- студент знает предложенные ему три вопроса.
Обозначим элементарные события:
- студент знает ответ на первый вопрос;
- студент знает ответ на второй вопрос;
- студент знает ответ на третий вопрос.
1 способ
Событие 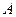заключается в следующем: студент знает ответ на первый вопрос, и 
студент знает ответ на второй вопрос, и 
студент знает ответ на третий вопрос: 
,
где , и - зависимые события, так как билеты с вопросами не возвращаются обратно.
Применим теорему о вероятности произведения зависимых событий и получим:
.
2 способ
Задачу можно решить по классической формуле вероятности:
,
где общее число исходов опыта 
равно числу выборок из 25 вопросов по 3 вопроса, которые отличаются одна от другой только самими вопросами, при этом порядок следования вопросов значения не имеет. Такие выборки из 25 элементов по 3 элемента называются сочетаниями без возвращения (без повторения элементов) и вычисляются по формуле: 
.
Число исходов, благоприятствующих появлению события 
, равно числу сочетаний из 20 вопросов по три вопроса и вычисляется по формуле: 
(из 20 известных вопросов студенту достались 3 вопроса, а из 5 неизвестных не досталось ни одного).
Задача 8. В цехе работают 7 мужчин и 3 женщины. По табельным номерам наудачу отобраны три человека. Найти вероятность того, что все отобранные лица окажутся мужчинами.
Событие 
-все отобранные лица окажутся мужчинами.
Составим элементарные события:
- первый отобранный рабочий – мужчина;
- второй отобранный рабочий – мужчина;
- третий отобранный рабочий – мужчина.
1 способ
Событие заключается в следующем: первый отобранный рабочий – мужчина, и 
второй отобранный рабочий – мужчина, и третий отобранный рабочий – мужчина: 
,
где , и - зависимые события, так как отобранные лица в список не возвращаются.
Применим теорему о вероятности произведения зависимых событий и получим:
.
2 способ
Задачу можно решить по классической формуле вероятности:
,
где общее число исходов опыта равно числу выборок из 10 рабочих по 3 рабочих, которые отличаются одна от другой только самими рабочими, при этом порядок следования рабочих значения не имеет. Такие выборки из 10 элементов по 3 элемента называются сочетаниями без возвращения (без повторения элементов) и вычисляются по формуле: 
.
Число исходов, благоприятствующих появлению события , равно числу сочетаний из 7 мужчин по три мужчины и вычисляется по формуле: 
(из семи мужчин наудачу выбрали троих и из трех женщин не выбрали ни одной).
Задача 9. На полке в случайном порядке расставлены 15 учебников, причем пять из них в переплете. Библиотекарь берет наудачу три учебника.
Найти вероятность того, что хотя бы один из учебников окажется в переплете.
Событие - хотя бы один из трех выбранных учебников окажется в переплете;
Событие 
(не ) -ни один из трех выбранных учебников не будет в переплете.
Противоположные события и образуют полную группу несовместных событий.
Следовательно, 
.
Обозначим элементарные события:
- первый учебник в переплете;
- первый учебник без переплета;
- второй учебник в переплете;
- второй учебник без переплета;
- третий учебник в переплете;
- третий учебник без переплета.
1 способ
Событие (не ) заключается в следующем: первый взятый с полки учебник оказался без переплета, и второй учебник без переплета, и третий учебник без переплета: 
,
где , и - зависимые события, так как взятые с полки учебники не возвращаются обратно на полку.
Применим теорему о вероятности произведения зависимых событий и получим:
.
2 способ
Задачу можно решить по классической формуле вероятности:
.
3 способ
=
.
Задачи
1. Участок электрической цепи состоит из трех элементов 
. Вероятность выхода из строя каждого элемента за время 
равна 0,2. Какова вероятность разрыва цепи за время 
?
Ответ: 0,232.
2. Игра между игроками и 
ведется на следующих условиях: в результате первого хода, который всегда делает , он может выиграть с вероятностью 0,3. Если первым ходом не выигрывает, то ход делает и может выиграть с вероятностью 0,5. Если в результате этого хода 
не выигрывает, то делает второй ход, который может привести его к выигрышу с вероятностью 0,4.
Определить вероятность выигрыша для и .
Ответ: 0,44; 0,35.
3. Иван и Петр поочередно бросают монету. Выигрывает тот, у кого раньше появится герб. Иван бросает монету первым. Найти вероятности выигрыша для каждого из игроков, считая, что бросание монеты может продолжаться неограниченно долго.
Ответ: 
.
4. Для сигнализации об аварии установлены два независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство - равна 0,95, второе – 0,9. Найти вероятность того, что при аварии сработает: 1) только одно устройство; 2) хотя бы одно устройство; 3) оба устройства; 4) не сработает ни одно устройство.
Ответ: 0,14; 0,995; 0,855; 0,005.
5. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадет: 1) только один из стрелков; 2) хотя бы один из стрелков.
Ответ: 0,38; 0,94.
6. В электрическую цепь последовательно включены три элемента, работающие независимо друг от друга. Вероятности отказов первого, второго и третьего элементов равны: 0,1; 0,15; 0,2. Найти вероятность того, что тока в цепи не будет.
Ответ:0,388.
7. Три исследователя независимо один от другого производят измерение некоторой физической величины. Вероятность того, что первый исследователь допустит ошибку при считывании показаний прибора, равна 0,1. для второго и третьего исследователей эта вероятность соответственно равна 0,15 и 0,2. Найти вероятность того, что при однократном измерении хотя бы один из исследователей допустит ошибку.
Ответ: 0,388.
8. В мешочке содержится 10 одинаковых кубиков с номерами от 1 до 10. Наудачу извлекают по одному три кубика. Найти вероятность того, что последовательно появятся кубики с номерами 1, 2, 3, если кубики извлекаются: 1) без возвращения; 2) с возвращением (извлеченный кубик возвращается в мешочек).
Ответ: 
; 0,001.
9. В ящике 10 деталей, среди которых шесть окрашенных. Сборщик наудачу извлекает четыре детали. Найти вероятность того, что все извлеченные детали окажутся окрашенными.
Ответ: 
.
10. Из 20 экзаменационных билетов три содержат простые вопросы. Пять студентов по очереди берут билеты. Найти вероятность того, что хотя бы одному из них достанется билет с простыми вопросами.
Ответ: 0,601.
11. Вероятность попадания стрелком в десятку при одном выстреле равна 0,7, а в девятку – 0,3. Определить вероятность того, что стрелок при трех выстрелах наберет не менее 29 очков.
Ответ: 0,784.
12. Двенадцать деталей, среди которых три неисправные, укладываются в коробки по 4 детали. Найти вероятность того, что в каждой коробке будет одна неисправная деталь.
Ответ: 0,29.
13. Вероятность своевременного прибытия первого поезда дальнего следования равна 0,95; второго – 0,9; третьего – 0,8. Найти вероятность того, что только один поезд прибудет вовремя.
Ответ: 0,032.
14. В корзине лежат 20 теннисных мячей, из них 12 новых и 8 игранных. Из корзины извлекают наудачу два мяча для игры. Найти вероятность того, что оба мяча будут новыми.
Ответ: 0,347.
15. В коробке 5 синих, 4 красных и 3 зеленых карандаша. Наудачу вынимают три карандаша. Найти вероятность того, что все они одного цвета.
Ответ: 0,068.
16. Студент знает 20 из 25 вопросов программы. Зачет считается сданным, если студент ответит не менее, чем на три из четырех поставленных в билете вопросов. Взглянув на первый вопрос билета, студент обнаружил, что он его знает. Какова вероятность того, что студент сдаст зачет?
Ответ: 0,901.
17. Мастер, имея десять деталей, из которых три нестандартные, проверяет детали одну за другой, пока не попадется стандартная. Какова вероятность, что он проверит ровно две детали?
Ответ: 0,23.
18. Студент пришел на экзамен, зная 30 из 40 вопросов программы. В каждом билете три вопроса. Найти вероятность того, что студент ответит правильно: 1) на все вопросы наудачу взятого билета;
2) хотя бы на два вопроса.
Ответ: 0,41; 0,85.
