При качении тела по поверхности другого тела возникает сила, называемая силой трения качения, которая препятствует качению.
Как показывает опыт, эта сила при тех же материалах соприкасаемых тел всегда меньше трения скольжения.
Причины появления силы трения качения понятны из следующих рассуждений. Пусть на горизонтальной плоскости покоится цилиндр. Под действием силы, прижимающей цилиндр к плоскости (этой силой может быть сила тяжести), цилиндр и плоскость деформируются. Для простоты рассуждений будем считать, что деформируется только плоскость. Это упрощение мало повлияет на результат рассуждений. Силы упругости, действующие на каждый малый элемент цилиндра со стороны плоскости, будут симметричны относительно вертикальной плоскости АА, проходящей через ось цилиндра О (рис. 2.1). Поэтому результирующая сила «реакции опоры» вертикальна и проходит через ось цилиндра. Она и уравновешивает силу тяжести (рис. 2.1, а).
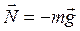 (2.1)
(2.1)
При движении цилиндра по плоскости картина распределения элементарных сил упругости существенно меняется. Это происходит по следующим причинам.
Всякая деформация твердого тела в какой-то степени неупругая, так как абсолютно упругих тел в природе не существует. Хотя при малых деформациях реальных твердых тел остаточные деформации весьма малы и ими обычно пренебрегают, здесь они приобретают принципиальное значение и пренебрегать ими нельзя.
Все реальные тела обладают свойством после упругого действия, состоящим в том, что тела не сразу восстанавливают свои формы после снятия нагрузки.
При движении цилиндра эти факторы проявляются в том, что деформация плоскости качения становится несимметричной (рис. 2.1, б).
Сзади цилиндра деформация плоскости не исчезает или исчезает лишь спустя некоторое время. Поэтому равнодействующая всех элементарных сил реакции плоскости оказывается наклоненной к поверхности качения и не проходит через ось цилиндра. Можно простыми рассуждениями прийти к заключению, что результирующая сила 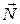 реакции плоскости должна проходить впереди оси, как показано на рис. 2.1, б.
реакции плоскости должна проходить впереди оси, как показано на рис. 2.1, б.
 |
При этом момент силы препятствует движению. Точка С приложения силы
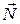 смещается в сторону движению на некоторое расстояние. Угол β и смещение, как показывает опыт очень малы. Разложим силу
смещается в сторону движению на некоторое расстояние. Угол β и смещение, как показывает опыт очень малы. Разложим силу 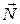 реакции плоскости на нормальную
реакции плоскости на нормальную 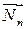 и касательную
и касательную 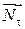 - составляющие к плоскости качения. Так как угол β мал, то
- составляющие к плоскости качения. Так как угол β мал, то 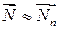 , а
, а 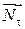 направлено почти по касательной к ободу колеса.
направлено почти по касательной к ободу колеса.
Касательная составляющая 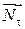 есть как раз та сила, которая препятствует движению цилиндра. Ее и называют силой трения качения. Действия силы трения качения вызывает нагревание контактирующих тел.
есть как раз та сила, которая препятствует движению цилиндра. Ее и называют силой трения качения. Действия силы трения качения вызывает нагревание контактирующих тел.
Если цилиндр или шар движется без ускорения, то должно выполняться правило равенства моментов. Момент силы трения качения относительно точки О равен произведению силы реакции опоры N на расстояние смещения k вследствие контактных деформаций точки приложения:
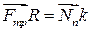 , (2.2)
, (2.2)
где k – плечо силы 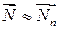 , R – радиус цилиндра.
, R – радиус цилиндра.
Отсюда для силы трения качения получаем следующее выражение:
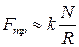 . (2.3)
. (2.3)
Величину k называют коэффициентом трения качения. Это выражение называется законом Амонтона-Кулона. Коэффициент трения качения, таким образом, представляет собой плечо силы 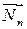 и имеет размерность длины.
и имеет размерность длины.
В данной работе коэффициент трения качения шара по плоскости определяется методом наклонного маятника.
Выведем формулу, которая связывает уменьшение амплитуды колебаний с углом наклона маятника. При качении шара по плоскости сила трения совершает работу. Эта работа уменьшает полную энергию шара. Полная энергия равна сумме кинетической и потенциальной энергии шара относительно положения равновесия. В тех положениях, где маятник максимально отклонен от положения равновесия, его скорость равна нулю; следовательно, и кинетическая энергия также равна нулю. Эти точки называются точками поворота. В них маятник останавливается, поворачивается и движется обратно. В момент поворота энергия маятника равна потенциальной энергии, поэтому уменьшение потенциальной энергии маятника при его движении от одной точки поворота до другой равна работе силы трения на пути между точками поворота.
Пусть А – точка поворота (рис. 2.2, а). В этом положении нить маятника составляет угол α с осью ОО´. Если бы трения не было, то через половину периода маятник оказался бы в точке N, а угол отклонения был бы равен α. Но из-за трения шар немного не докатится до точки N и остановится в точке В. Это и будет точка поворота. В этой точке угол нити с осью ОО´ будет α – Δα. За половину периода угол поворот маятника уменьшился на Δα. Точка В расположена несколько ниже, чем точка А, и поэтому потенциальная энергия маятника в точке В меньше, чем в точке А. Следовательно, маятник потерял высоту при перемещении из А в В.
Найдем связь между потерей угла Δα и потерей высоты Δ h.
Для этого спроецируем точки А и В на ось ОО´ (рис. 2.2, б). Это будут точки А´ и В соответственно. Очевидно, что длина отрезка
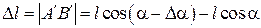 ,
,
где l – длина нити, равная радиусу дуги АВ окружности. При этом угол этой дуги равен (2α–Δα).
Так как ось ОО´ наклонена под углом β к горизонту, то проекция отрезка Δ l на вертикальную ось и есть потеря высоты Δ h:
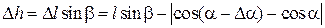 (2.4)
(2.4)
При этом изменение потенциальной энергии маятника между точками А и В равно
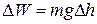 (2.5)
(2.5)
где m – масса шара, g – ускорение свободного падения.
Вычислим работу силы трения. Так как сила трения равна
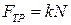 (2.6)
(2.6)
где k – коэффициент трения, 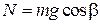 – сила нормального давления шара на плоскость, то работа силы трения на пути
– сила нормального давления шара на плоскость, то работа силы трения на пути
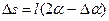
между точками А и В равна
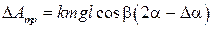 (2.7)
(2.7)
Так как 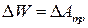 , то из уравнения (2.4), (2.5) и (2.7) получаем
, то из уравнения (2.4), (2.5) и (2.7) получаем
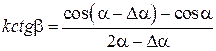 (2.8)
(2.8)
Выражение (2.8) можно существенно упростить, если учесть, что угол Δα очень мал (как мы уже отмечали, он порядка 10–2).
Так как 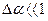 , то cosΔα ≈1, sinΔα≈Δα и cos(α – Δα), тогда
, то cosΔα ≈1, sinΔα≈Δα и cos(α – Δα), тогда
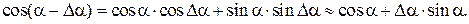
Поэтому формулу (2.8) можно записать так:
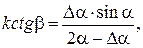
откуда
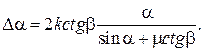 (2.9)
(2.9)
Из формулы (2.9) видно, что потеря угла за одну половину периода определяется величиной k и углом α. Однако можно найти такие условия, при которых Δα от угла α не зависит.
 |
Вспомним, что k мало, порядка 10–3. Если рассматривать достаточно большие амплитуды α так, чтобы sin α >> k ctg β, то слагаемые
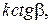 в знаменателе формулы (2.9) можно пренебречь и тогда
в знаменателе формулы (2.9) можно пренебречь и тогда
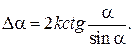
С другой стороны, пусть углы α будут малыми, т.е. α <<1 и 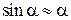 тогда за половину колебания потеря угла равна
тогда за половину колебания потеря угла равна
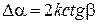 (2.10)
(2.10)
Заметим, что формула (2.10) справедлива при условии
k ctg β << sin α << 1 (2.11)
Из-за того, что k ~10–2, углы α~(10–2  10–1) радиан удовлетворяют неравенствам (2.11).
10–1) радиан удовлетворяют неравенствам (2.11).
Если бы k был порядка 10–2  10–1, как в случае трения скольжения, то тогда бы неравенства (2.11) не выполнялись. Понятно, что за одно полное колебание потеря угла будет
10–1, как в случае трения скольжения, то тогда бы неравенства (2.11) не выполнялись. Понятно, что за одно полное колебание потеря угла будет 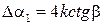 , а за n колебаний потеря угла составляет:
, а за n колебаний потеря угла составляет:
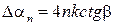
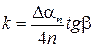 . (2.12)
. (2.12)
Формула (2.12) дает удобный способ измерения k: необходимо измерить уменьшение угла Δαn за 5-15 колебаний.
 2020-05-25
2020-05-25 185
185








