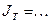Общий вид установки изображен на рис.6.2. Подставка 1 оснащена регулируемыми ножками 2, которые позволяют сделать выравнивание прибора. На подставке закреплена колонна 3, к которой прикреплен неподвижный верхний кронштейн 4 и подвижной нижний кронштейн 5. На верхнем кронштейне находится электромагнит 6, фотоэлектрический датчик №1 (7) и вороток 8 для закрепление и регулирования длины бифилярной подвески маятника. Нижний кронштейн вместе с прикрепленным к нему фотоэлектрическим датчиком №2 (9) можно перемещать вдоль колонны и фиксировать в произвольно выбранном положении. Маятник 10 прибора - это ролик, закрепленный на оси и подвешенный на бифилярном подвесе, на который накладываются сменные кольца 11, изменяя таким образом момент инерции системы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Задание 1
1. Намотать на ось маятника нить подвески, обращая внимание на то, чтобы она обматывалась равномерно - виток к витку. Фиксировать маятник с помощью электромагнита, обращая внимание на то, чтобы нить при этом положении была не очень затянута. Вернуть маятник в направлении его движения на угол около 50. Нажать клавишу "Сброс". Нажать клавишу «Пуск». Посчитать измеренное значение времени падения маятника. Провести измерение времени не менее 5 раз. По шкале на вертикальной колонне прибора определить длину маятника.
Данные занести в таблицу 6.1.
Таблица 6.1 – Расчет экспериментального значения момента инерции 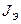 маятника Максвелла
маятника Максвелла
| t 1 = (с) | t 2 = (с) | t 3 = (с) | t 4 = (с) | t 5 = (с) |
|
| ||||
|
| ||||
2. Измерить параметры маятника. Данные занести в таблицу 6.2.
Таблица 6.2 – Расчет теоретического значения момента инерции 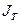 маятника Максвелла
маятника Максвелла
| Масса, (кг) | Линейные размеры, (м) | Моменты инерции, кг·м2 | |
| Момент инерции стержня (оси) | m0= | D0 = | 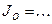
|
| Момент инерции диска | mD= | DD = | 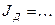
|
| Момент инерции кольца | m k= | Dk = | 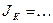
|
| Момент инерции маятника |
| ||
3. Определить массу маятника вместе с кольцом по формуле:
 (6.9)
(6.9)
где m0 - масса оси маятника;
mk - масса кольца;
mD - диска.
4. По формуле (6.8) определить момент инерции маятника 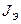 .
.
5. Вычислить относительную и абсолютную ошибки его определения 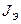 (см. Приложение А):
(см. Приложение А):
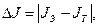
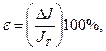
6. Теоретическое значение, рассчитанное по формуле:
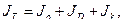
где J o – момент инерции оси маятника;
J D – момент инерции ролика;
J к – момент инерции кольца.
Значение отдельных моментов инерции определяются по формулам:
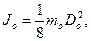
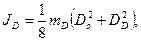
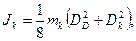
Окончательный результат представьте в виде:
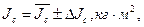
Задание 2
1. Определить с помощью маятника Максвелла силу сопротивления воздуха.
2. Согласно закону сохранения энергии: 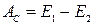
т.е. работа силы трения равна изменению полной механической энергии
3. По определению механической работы: 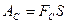 ,
,
где S – перемещение тела, FС – сила сопротивления воздуха.
4. Изменение полной механической энергии равно изменению потенциальной энергии маятника: 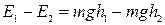 , где h 1 – расстояние, на которое маятник опустится за один ход, h 2 – расстояние, на которое маятник опустится за следующий ход, m – масса маятника.
, где h 1 – расстояние, на которое маятник опустится за один ход, h 2 – расстояние, на которое маятник опустится за следующий ход, m – масса маятника.
5. Тогда перемещение маятника будет равно: 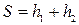 .
.
6. Следовательно, сила сопротивления воздуха рассчитывается по формуле:
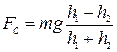 .
.
7. Опыт повторить 5 раз. Полученные значения занести в таблицу 6.3.
 2020-05-25
2020-05-25 158
158

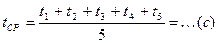
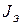 = (кг·м2)
= (кг·м2)