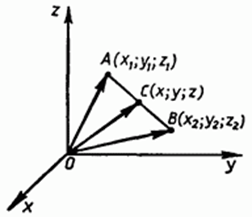
а) Координаты середины отрезка. В системе координат Охуz отметим точку А с координатами (х1;у1; z1), и точку В с координатами (х2; у2; z2). Выразим координаты (х; у; z) середины С отрезка АВ через координаты его концов (рис. 128). Так как точка С — середина отрезка АВ, то 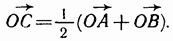 (2) (Справедливость этого равенства доказана в курсе планиметрии.)
(2) (Справедливость этого равенства доказана в курсе планиметрии.)
Координаты векторов 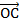 ,
, 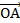 и
и 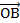 равны соответствующим координатам трех точек С, А и В:
равны соответствующим координатам трех точек С, А и В: 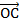 {х; у; z }
{х; у; z } 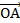 {х1; у1; z 1}
{х1; у1; z 1} 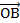 {х2; у2; z 2}. Записав равенство (2) в координатах, получим
{х2; у2; z 2}. Записав равенство (2) в координатах, получим
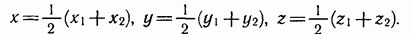
Таким образом, каждая координата середины отрезка равна полусумме соответствующих координат его концов.
Б) Вычисление длины вектора по его координатам.
Докажем, что длина вектора 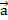 {х; у; z} вычисляется по формуле
{х; у; z} вычисляется по формуле 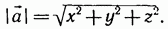 (3)
(3)
Отложим на осях координат векторы 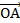 1 = х
1 = х 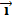 ,
, 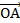 2 = y
2 = y 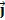 ,
, 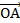 3 = z
3 = z 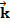 .
.
и рассмотрим вектор 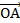 =
= 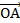 1 +
1 + 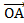 2 +
2 + 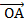 3 = х
3 = х 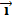 + y
+ y 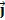 + z
+ z 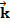
Длина вектора 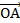 выражается через длины векторов
выражается через длины векторов 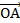 1,
1, 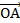 2 ,
2 , 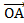 3 следующим образом:
3 следующим образом:
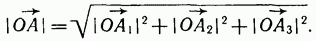 (4)
(4)
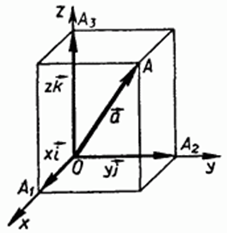
В самом деле, если точка А не лежит на координатных плоскостях (рис. 129), то равенство (4) справедливо в силу свойства диагонали прямоугольного параллелепипеда:
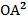 =
= 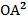 1 +
1 + 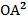 2 +
2 + 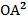 3
3
Во всех других случаях расположения точки А (точка А лежит на координатной плоскости или на оси координат) равенство (4) также верно (рассмотрите эти случаи самостоятельно).
Так как 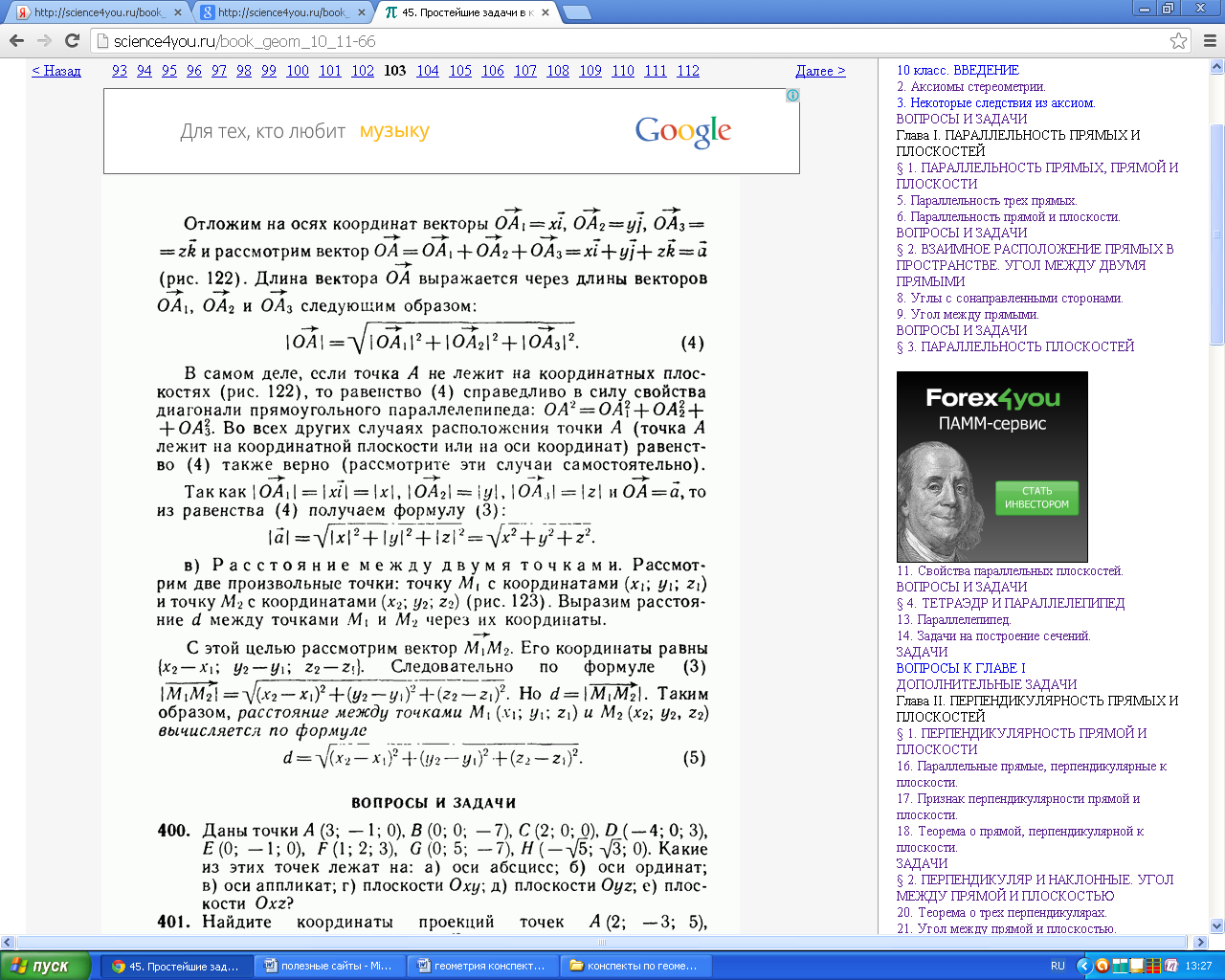 , то из равенства (4) получаем формулу (3):
, то из равенства (4) получаем формулу (3):
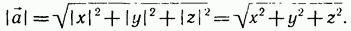
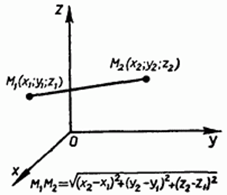
в) Расстояние между двумя точками. Рассмотрим две произвольные точки: точку М1 с координатами (х1; у1; z1) и точку М2 с координатами (х2; у2; z2).
Выразим расстояние d между точками М1 и М2 через их координаты.
С этой целью рассмотрим вектор 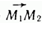 Его координаты равны {х2 – х1; у2 – у1; z2 – z1}.
Его координаты равны {х2 – х1; у2 – у1; z2 – z1}.
Следовательно по формуле (3)  . Но
. Но  Таким образом, расстояние между точками М1 (х1; у1; z1) и М2 (х2; у2; z2) вычисляется по формуле
Таким образом, расстояние между точками М1 (х1; у1; z1) и М2 (х2; у2; z2) вычисляется по формуле
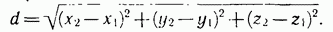
 2020-05-21
2020-05-21 289
289








