Возьмем два произвольных вектора  и
и 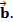 Отложим от какой-нибудь точки О векторы
Отложим от какой-нибудь точки О векторы  =
=  и
и  =
=  . Если векторы
. Если векторы  и
и  не являются сонаправленными, то лучи ОА и ОВ образуют угол АОВ (рис. 133).
не являются сонаправленными, то лучи ОА и ОВ образуют угол АОВ (рис. 133).


Рис. 133 Рис 134
Градусную меру этого угла обозначим буквой α и будем говорить, что угол между векторами  и
и  равен α. Если же векторы
равен α. Если же векторы  и
и  сонаправлены, в частности один из них или оба нулевые, то будем считать, что угол между ними равен 0°. Если угол между векторами равен 90°, то векторы называются перпендикулярными. Угол между векторами
сонаправлены, в частности один из них или оба нулевые, то будем считать, что угол между ними равен 0°. Если угол между векторами равен 90°, то векторы называются перпендикулярными. Угол между векторами  и
и  обозначается так:
обозначается так: 
На рисунке 134 изображено несколько векторов. Углы между ними таковы:  . На этом рисунке
. На этом рисунке 
Скалярное произведение векторов.
Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
Скалярное произведение векторов 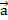 и
и  обозначается так:
обозначается так: 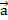 ·
·  Таким образом,
Таким образом,  . Как и в планиметрии, справедливы утверждения:
. Как и в планиметрии, справедливы утверждения:
|
|
|
скалярное произведение ненулевых векторов равно нулю и только тогда, когда эти векторы перпендикулярны;
скалярный квадрат вектора (т. е. скалярное произведения вектора на себя) равен квадрату его длины. (Докажите эти утверждения самостоятельно).
Скалярное произведение двух векторов можно вычислить координаты этих векторов: скалярное произведение векторов  выражается формулой
выражается формулой
 Это утверждение доказывается точно так же, как в планиметрии.
Это утверждение доказывается точно так же, как в планиметрии.
Косинус угла α между ненулевыми векторами  вычисляется по формуле
вычисляется по формуле

В самом деле, так как  , то
, то  .
.
Подставив сюда выражения для  через координат векторов
через координат векторов 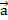 и
и  , получим формулу (1).
, получим формулу (1).
Сформулируем основные свойства скалярного произведение векторов.
Для любых векторов 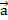 ,
, 
 и любого числа k справедливо равенства:
и любого числа k справедливо равенства:

 2020-05-21
2020-05-21 352
352








