2020-05-21
378
Лекция
ДЕКАРТОВА ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ
В ПРОСТРАНСТВЕ
Содержание учебного материала:
Изучение декартовой системы координат в пространстве, построение по заданным координатам точек и плоскостей, нахождение координат точек и векторов:
1.Понятие прямоугольного базиса в пространстве.
2.Декартова прямоугольная система координат в пространстве.
3.Координаты точки и вектора в пространстве.
Изучение свойств векторных величин, правил разложения векторов в трехмерном пространстве, правил нахождения координат вектора в пространстве, правил действий с векторами, заданными координатами.
4.Разложение вектора по трём некомпланарным направлениям:
а) разложение радиус-вектора по базису;
б) разложение произвольного вектора по базису;
5. Действия над векторами в координатной форме.
6. Изображение точки и вектора в прямоугольной системе координат.
Прямоугольный базис в пространстве.
Для построения прямоугольного базиса в пространстве нужно:
- провести три взаимно перпендикулярных прямые х, у, z, пересекающихся в одной точке О;
| у |
| х |
| z |
| Мz |
| Му |
| Мх |
| О |
| ху |
| хz |
| уz |
| Рис. 1 |
| М |
|
Плоскость, проходящая через прямые х и у, называют плоскостью ху, две другие плоскости соответственно хz и уz.
Прямые х, у, z называются координатными осями, х – ось абсцисс, у – ось ординат, z – ось аппликат. Точка пересечения О – начало координат, плоскости ху, хz, уz – координатные плоскости. Точка О разбивает каждую из этих осей на две полуоси, одна из которых положительная, а другая отрицательная (рис. 1).
Пусть 
– единичный вектор оси абсцисс, 
- единичный вектор оси ординат,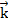 
- единичный вектор оси аппликат.
Тройка взаимно перпендикулярных, единичных векторов (i, j, k), отложенных от начала координат точки О и по направлению совпадающих с координатными осями, называют прямоугольным базисом в пространстве.
Декартова прямоугольная система координат в пространстве.
Совокупность прямоугольного базиса и начала координат называют прямоугольной системой координат в пространстве.
