2020-05-25
118
Уравнение 
определяет плоскость, проходящую через точку 
и имеющую нормальный вектор 
– уравнение плоскости в отрезках
. Расстояние d от точки 
до плоскости 
равно 
Угол между прямыми 
- прямая лежит в плоскости.
- прямая и плоскость пересекаются
Угол между прямой и пл 
общее уравнение пл
Угол между плоскостями 
14. Эллипс.
Общее уравнение эллипса 
Если центр эллипса находится в начале координат и фокусы эллипса находятся на оси 
на равных расстояниях от начала координат, то уравнение примет вид 
Эксцентриситет 
и коэффициент сжатия эллипса 
связаны соотношением 
15. Гипербола.
Если поместить фокусы гиперболы в точках 
то получается каноническое уравнение гиперболы
где 
Вершинами гиперболы являются точки 
тогда 
действительная ось гиперболы, 
мнимая ось гиперболы.
Гипербола имеет две асимптоты 
Эксцентриситет гиперболы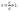 
Фокальные радиус-векторы
16. Парабола.
Если директрисой параболы является прямая 
а фокусом является точка 
то уравнение параболы имеет вид 
Парабола симметрична относительно оси абсцисс 
Комплексные числа.
Алгебраическая форма комплексного числа
.
- алгебраическая форма комплексного числа.
комплексные числа 
называются комплексно сопряженными
геометрическая интерпретация: комплексно-сопряженные числа 
и 
отождествляются с точками (х,у) и (х,-у), симметричными относительно оси Ох.
Свойства комплексно-сопряженных чисел:
1. 
.
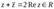2. 
.
3. 
.
4. 
18. Дробно-рациональная функция. Разложение правильной дроби на простейшие дроби.
Пусть 
- правильная рациональная дробь, Q (x) – многочлен степени n с коэффициентом перед старшей неизвестной равным единице (для простоты): Q (x)= xn + b 1 xn- 1+…+ bn. Q (x) имеет n действительных и комплексных корней. Так как у Q (x) коэффициенты – действительные числа, то комплексные корни попарно сопряжены.
Если Q (x) – многочлен степени n с действительными коэффициентами, то его можно разложить 
