Лекция 23
Приложения определенного интеграла.
1. Вычисление площадей плоских фигур в декартовых
координатах
- Вычисление площади плоской фигуры в полярных координатах.
- Вычисление объемов тел.
- Вычисление длины дуги.
Применение определенных интегралов к вычислению площадей плоских фигур основано на геометрическом смысле определенного интеграла как площади криволинейной трапеции, ограничено отрезком [ a;b ], прямыми x=a, x=b и кривой y=f(x) ³0.
Другими словами, в декартовой системе координат за основную фигуру, площадь которой выражается одним интегралом, принимается криволинейная трапеция.
а) 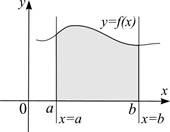
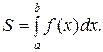
б) 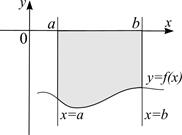
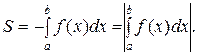
в) 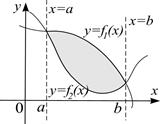 Если f1(x)³ f2(x) на [ a;b ], то
Если f1(x)³ f2(x) на [ a;b ], то
S=S1 – S2.

г) 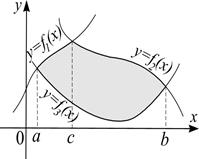 Если фигура АВСВ1 не является криволинейной трапецией, то представляют ее как сумму криволинейных трапеций:
Если фигура АВСВ1 не является криволинейной трапецией, то представляют ее как сумму криволинейных трапеций:
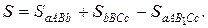
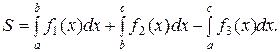
Пример 6.20
1) С помощью определенного интеграла вычислить площади фигур, ограниченных следующими линиями:
1) 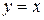 ,
, 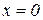 ,
, 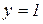 ,
, 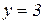 ;
;
2) 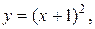
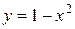 ,
, 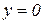 ;
;
3) одной аркой циклоиды 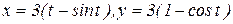 ;
;
4) лемнискатой Бернулли 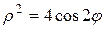 .
.
Решение
1) Построим фигуру, площадь которой необходимо найти (чертеж 1). Фигура 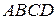 является криволинейной трапецией, прилежащей к оси
является криволинейной трапецией, прилежащей к оси 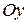 , ограниченной «сверху» графиком функции
, ограниченной «сверху» графиком функции 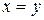 , «снизу» - отрезком
, «снизу» - отрезком 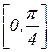 оси
оси 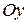 , на который проецируется данная фигура.
, на который проецируется данная фигура.
Искомую площадь найдем по формуле
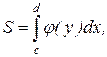
где 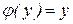 ,
, 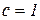 ,
, 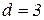 .
.
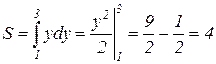 (ед.2).
(ед.2).
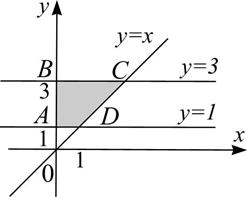
Чертеж 1
2) Построим фигуру, площадь которой необходимо найти. Напомним, что и 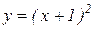 , и
, и 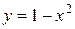 являются уравнениями парабол (чертеж 2). Точки пересечения парабол найдем, решив систему:
являются уравнениями парабол (чертеж 2). Точки пересечения парабол найдем, решив систему:
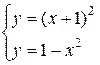
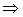
 (-1;0),
(-1;0), 
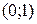 .
.
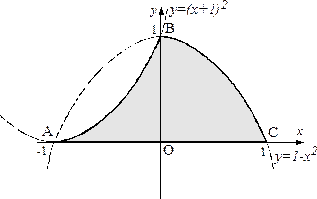 Чертеж 2 Чертеж 2 | 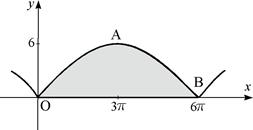 Чертеж 3 Чертеж 3 |
Нам необходимо вычислить площадь фигуры 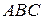 , которая не является криволинейной трапецией, но её площадь может быть составлена из площадей криволинейных трапеций
, которая не является криволинейной трапецией, но её площадь может быть составлена из площадей криволинейных трапеций 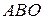 и
и 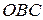 , прилежащих к оси
, прилежащих к оси 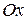 . Криволинейная трапеция
. Криволинейная трапеция 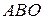 ограничена «сверху» параболой
ограничена «сверху» параболой 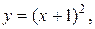 «снизу» - отрезком
«снизу» - отрезком 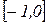 оси
оси 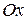 , а криволинейная трапеция
, а криволинейная трапеция 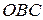 - параболой
- параболой 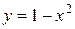 и отрезком
и отрезком 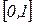 .
.
Тогда искомая площадь равна
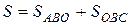 =
= 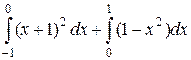 =
= 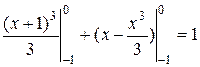 (ед.2).
(ед.2).
3) В этом случае кривая (циклоида) задана параметрическими уравнениями 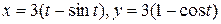 . Для построения циклоиды (чертеж 3) воспользуемся Приложением Б. Точкам
. Для построения циклоиды (чертеж 3) воспользуемся Приложением Б. Точкам 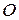 ,
, 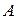 и
и 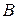 соответствуют значения параметра
соответствуют значения параметра 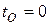 ,
, 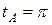 и
и 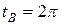 .
.
Данная фигура является криволинейной трапецией, прилежащей к оси 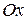 , ограничена параллельными прямыми
, ограничена параллельными прямыми 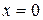 и
и 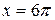 (каждая из прямых вырождается в точку), «сверху» ограничена графиком циклоиды, «снизу» – отрезком
(каждая из прямых вырождается в точку), «сверху» ограничена графиком циклоиды, «снизу» – отрезком 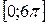 оси
оси 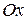 , поэтому, согласно формуле вычисления площади фигуры при параметрическом задании кривой, имеем
, поэтому, согласно формуле вычисления площади фигуры при параметрическом задании кривой, имеем
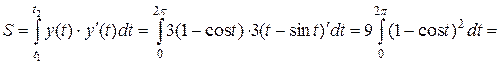
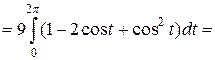
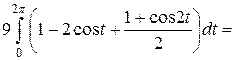
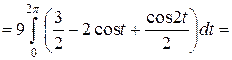
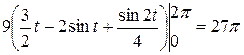 (ед.2).
(ед.2).
Вычисление площади плоской фигуры в полярных координатах.
Пусть кривая задана уравнением в полярных координатах: r=f(j). Рассмотрим криволинейный сектор, ограниченный лучами j=a, j=b и кривой r=f(j).
Определим площадь этого сектора.
Разобьем сектор произвольным образом на n частей лучами a=j0< j1<…< jn=b; ∆ ji=ji -ji-1. Заменим каждый частичный криволинейный сектор круговым. Для этого выберем на каждом участке [ ji-1; ji ] точку qi и между лучами j=ji-1 и j=ji построим круговой сектор радиуса f(qi).
Площадь кругового сектора равна 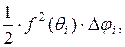 а сумма всех таких секторов равна
а сумма всех таких секторов равна 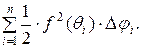
Обозначим 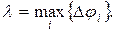
Предел этой суммы при условии, что наибольший из углов l ®0, и дает искомую площадь криволинейного сектора: 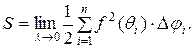
Но, с другой стороны, этот предел, согласно определению определенного интеграла, дает 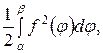 поэтому получим формулу:
поэтому получим формулу:
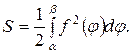
Пример 6.21
Кривая 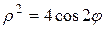 (лемниската Бернулли) задана в полярной системе координат. Для ее построения воспользуемся Приложением Б (чертеж 4).
(лемниската Бернулли) задана в полярной системе координат. Для ее построения воспользуемся Приложением Б (чертеж 4).
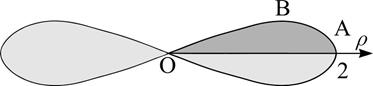 Чертеж 4 Чертеж 4 | В силу симметричности искомая площадь равна учетверенной площади криволинейного сектора 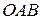 . . |
Дуга 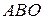 описывается концом полярного радиуса
описывается концом полярного радиуса 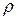 при изменении полярного угла
при изменении полярного угла 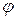 от 0 до
от 0 до 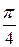 (для значений
(для значений 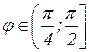 функция
функция 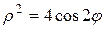 не определена). Поэтому, согласно формуле вычисления площади криволинейного сектора, имеем
не определена). Поэтому, согласно формуле вычисления площади криволинейного сектора, имеем
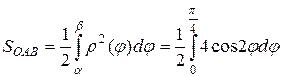 =
= 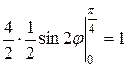 (ед.2).
(ед.2).
 (ед.2).
(ед.2).
 2020-05-21
2020-05-21 1524
1524