Найдём угол OKM: OKM = 90° − 83° = 7°. Треугольник OMK — равнобедренный, поэтому угол OMK равен углу OKM и равен 7°
8. Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB = 20, а расстояния от центра окружности до хорд AB и CD равны соответственно 24 и 10.
Решение.
 Проведём построения и введём обозначения, как показано на рисунке. Рассмотрим треугольники
Проведём построения и введём обозначения, как показано на рисунке. Рассмотрим треугольники  и
и  они прямоугольные, стороны
они прямоугольные, стороны  и
и  равны как радиусы окружностей,
равны как радиусы окружностей,  — общая, следовательно, треугольники
— общая, следовательно, треугольники  и
и  равны. Откуда
равны. Откуда  Аналогично, равны треугольники
Аналогично, равны треугольники  и
и  откуда
откуда  Рассмотрим треугольник
Рассмотрим треугольник  найдём
найдём 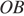 по теореме Пифагора:
по теореме Пифагора:

Рассмотрим треугольник  он прямоугольный, из теоремы Пифагора найдём
он прямоугольный, из теоремы Пифагора найдём 

Таким образом, 
Ответ: 48.
9. Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB = 18, CD = 24, а расстояние от центра окружности до хорды AB равно 12.
Решение.
 Проведём построения и введём обозначения, как показано на рисунке. Рассмотрим треугольники
Проведём построения и введём обозначения, как показано на рисунке. Рассмотрим треугольники  и
и  они прямоугольные, стороны
они прямоугольные, стороны  и
и  равны как радиусы окружностей,
равны как радиусы окружностей,  — общая, следовательно, треугольники
— общая, следовательно, треугольники  и
и  равны. Откуда
равны. Откуда 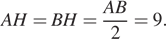 Аналогично, равны треугольники
Аналогично, равны треугольники  и
и  откуда
откуда  Рассмотрим треугольник
Рассмотрим треугольник  найдём
найдём  по теореме Пифагора:
по теореме Пифагора:

Рассмотрим треугольник  он прямоугольный, из теоремы Пифагора найдём
он прямоугольный, из теоремы Пифагора найдём 

Таким образом, расстояние от центра окружности до хорды  равно 9.
равно 9.
Ответ: 9.
10. На окружности с центром O отмечены точки A и B так, что ∠ AOB = 66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги.
Решение.
Пусть длина большей дуги  равна
равна  Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:
Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:
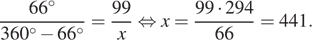
Ответ: 441.
11. 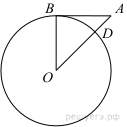
Отрезок AB = 40 касается окружности радиуса 75 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
Решение.
Радиус окружности перпендикулярен касательной в точке касания. Из прямоугольного треугольника  по теореме Пифагора найдём
по теореме Пифагора найдём 

Найдём 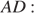

Ответ: 10.
12.  На отрезке AB выбрана точка C так, что AC = 75 и BC = 10. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC = 75 и BC = 10. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
Решение.
 Проведём радиус
Проведём радиус  в точку касания. Из прямоугольного треугольника
в точку касания. Из прямоугольного треугольника  по теореме Пифагора найдём
по теореме Пифагора найдём 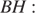

Ответ: 40.
13. 
Касательные в точках A и B к окружности с центром O пересекаются под углом 72°. Найдите угол ABO. Ответ дайте в градусах.
Решение.

Введём обозначение, как показано на рисунке. Касательные, проведённые к окружности из одной точки равны, поэтому  следовательно, треугольник
следовательно, треугольник  — равнобедренный. Откуда
— равнобедренный. Откуда  Угол между касательной и хордой равен половине дуги, которую он заключает, значит, дуга
Угол между касательной и хордой равен половине дуги, которую он заключает, значит, дуга  равна 108°. Угол AOB — центральный, поэтому он равен дуге, на которую опирается, следовательно, равен 108°. Рассмотрим треугольник AOB, он равнобедренный, следовательно,
равна 108°. Угол AOB — центральный, поэтому он равен дуге, на которую опирается, следовательно, равен 108°. Рассмотрим треугольник AOB, он равнобедренный, следовательно, 
Ответ: 36.
14. 
Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠ C, если ∠ A = 44°. Ответ дайте в градусах.
Решение.
Угол ABC — прямой, так как он вписанный и опирается на диаметр. Следовательно, треугольник ABC — прямоугольный, а 
Ответ: 46.
15.  Окружность вписана в квадрат. Найдите площадь квадрата.
Окружность вписана в квадрат. Найдите площадь квадрата.
Решение.
Сторона квадрата равна диаметру вписанной в него окружности, значит, площадь данного квадрата равна:

Ответ: 6084.
16. 
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Решение.

Проведём радиусы  и
и  в точки касания. Получили два прямоугольных треугольника, катет
в точки касания. Получили два прямоугольных треугольника, катет 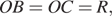 где
где  — радиус окружности, гипотенуза
— радиус окружности, гипотенуза  этих двух прямоугольных треугольников — общая, следовательно, эти треугольники равны. То есть, имеется равенство углов
этих двух прямоугольных треугольников — общая, следовательно, эти треугольники равны. То есть, имеется равенство углов

Теперь из треугольника 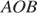 найдём радиус
найдём радиус 

Ответ: 4.
17. Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 7,5, а AB = 2.
Решение.
 Пусть О — центр окружности. Радиус окружности, проведённый в точку касания, перпендикулярен касательной. Поэтому треугольник OBA — прямоугольный. Найдём OA по теореме Пифагора:
Пусть О — центр окружности. Радиус окружности, проведённый в точку касания, перпендикулярен касательной. Поэтому треугольник OBA — прямоугольный. Найдём OA по теореме Пифагора:

Следовательно, длина стороны  равна
равна 
Ответ: 8.
18. 
Касательные в точках 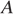 и
и  к окружности с центром
к окружности с центром  пересекаются под углом 76°. Найдите угол
пересекаются под углом 76°. Найдите угол 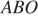 . Ответ дайте в градусах.
. Ответ дайте в градусах.
Решение.

Введём обозначение, как показано на рисунке. Касательные, проведённые к окружности из одной точки равны, поэтому  следовательно, треугольник
следовательно, треугольник  — равнобедренный. Откуда
— равнобедренный. Откуда 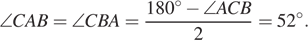 Угол между касательной и хордой равен половине дуги, которую он заключает, значит, дуга
Угол между касательной и хордой равен половине дуги, которую он заключает, значит, дуга  равна 104°. Угол AOB — центральный, поэтому он равен дуге, на которую опирается, следовательно, равен 104°. Рассмотрим треугольник AOB, он равнобедренный, следовательно,
равна 104°. Угол AOB — центральный, поэтому он равен дуге, на которую опирается, следовательно, равен 104°. Рассмотрим треугольник AOB, он равнобедренный, следовательно, 
Ответ: 38.
19. 
К окружности с центром в точке  проведены касательная
проведены касательная  и секущая
и секущая  . Найдите радиус окружности, если
. Найдите радиус окружности, если  ,
,  .
.
Решение.
Соединим отрезком точки O и B; полученный отрезок — радиус, проведённый в точку касания, поэтому OB перпендикулярен AB. Задача сводится к нахождению катета OB прямоугольного треугольника AOB: по теореме Пифагора равен 75.
Ответ: 75.
20. 
На отрезке  выбрана точка
выбрана точка  так, что
так, что  и
и  . Построена окружность с центром
. Построена окружность с центром 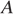 , проходящая через
, проходящая через  . Найдите длину отрезка касательной, проведённой из точки
. Найдите длину отрезка касательной, проведённой из точки 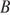 к этой окружности.
к этой окружности.
Решение.
 Проведём радиус
Проведём радиус  в точку касания. Из прямоугольного треугольника
в точку касания. Из прямоугольного треугольника 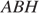 по теореме Пифагора найдём
по теореме Пифагора найдём 

Ответ: 63.
21. 
Отрезок  касается окружности радиуса 24 с центром
касается окружности радиуса 24 с центром  в точке
в точке 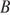 . Окружность пересекает отрезок
. Окружность пересекает отрезок  в точке
в точке 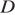 . Найдите
. Найдите  .
.
Решение.
Радиус окружности перпендикулярен касательной в точке касания. Из прямоугольного треугольника  по теореме Пифагора найдём
по теореме Пифагора найдём 

Найдём 

Ответ: 16.
22. 
На отрезке  выбрана точка
выбрана точка  так, что
так, что 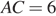 и
и  . Построена окружность с центром
. Построена окружность с центром 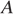 , проходящая через
, проходящая через  . Найдите длину отрезка касательной, проведённой из точки
. Найдите длину отрезка касательной, проведённой из точки 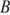 к этой окружности.
к этой окружности.
Решение.
 Проведём радиус
Проведём радиус 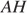 в точку касания. Из прямоугольного треугольника
в точку касания. Из прямоугольного треугольника  по теореме Пифагора найдём
по теореме Пифагора найдём 

Ответ: 8.
23. 
К окружности с центром в точке  проведены касательная
проведены касательная  и секущая
и секущая  . Найдите радиус окружности, если
. Найдите радиус окружности, если  ,
, 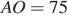 .
.
Решение.
Соединим отрезком точки O и B; полученный отрезок — радиус, проведённый в точку касания, поэтому OB перпендикулярен AB. Задача сводится к нахождению катета OB прямоугольного треугольника AOB: по теореме Пифагора равен  см.
см.
Ответ: 72.
24. 
Отрезок  касается окружности радиуса 54 с центром
касается окружности радиуса 54 с центром  в точке
в точке 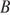 . Окружность пересекает отрезок
. Окружность пересекает отрезок  в точке
в точке  . Найдите
. Найдите 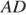 .
.
Решение.
Радиус окружности перпендикулярен касательной в точке касания. Из прямоугольного треугольника  по теореме Пифагора найдём
по теореме Пифагора найдём 

Найдём 

Ответ: 36.
25.  На отрезке
На отрезке  выбрана точка
выбрана точка  так, что
так, что  и
и  . Построена окружность с центром
. Построена окружность с центром 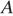 , проходящая через
, проходящая через  . Найдите длину отрезка касательной, проведённой из точки
. Найдите длину отрезка касательной, проведённой из точки  к этой окружности.
к этой окружности.
Решение.
 Проведём радиус
Проведём радиус 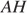 в точку касания. Из прямоугольного треугольника
в точку касания. Из прямоугольного треугольника  по теореме Пифагора найдём
по теореме Пифагора найдём 

Ответ: 45.
26. 
К окружности с центром в точке  проведены касательная
проведены касательная  и секущая
и секущая  . Найдите радиус окружности, если
. Найдите радиус окружности, если  ,
, 
Решение.
Соединим отрезком точки O и B; полученный отрезок — радиус, проведённый в точку касания, поэтому OB перпендикулярен AB. Задача сводится к нахождению катета OB прямоугольного треугольника AOB: по теореме Пифагора равен  см.
см.
Ответ: 24.
27. 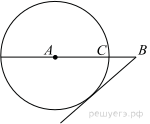 На отрезке
На отрезке  выбрана точка
выбрана точка  так, что
так, что  и
и  . Построена окружность с центром
. Построена окружность с центром 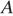 , проходящая через
, проходящая через  . Найдите длину отрезка касательной, проведённой из точки
. Найдите длину отрезка касательной, проведённой из точки 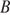 к этой окружности.
к этой окружности.
Решение.
 Проведём радиус
Проведём радиус  в точку касания. Из прямоугольного треугольника
в точку касания. Из прямоугольного треугольника 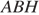 по теореме Пифагора найдём
по теореме Пифагора найдём 

Ответ: 24.
28.  На отрезке
На отрезке  выбрана точка
выбрана точка  так, что
так, что  и
и  . Построена окружность с центром
. Построена окружность с центром  , проходящая через
, проходящая через  . Найдите длину отрезка касательной, проведённой из точки
. Найдите длину отрезка касательной, проведённой из точки 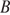 к этой окружности.
к этой окружности.
Решение.
 Проведём радиус
Проведём радиус 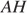 в точку касания. Из прямоугольного треугольника
в точку касания. Из прямоугольного треугольника 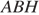 по теореме Пифагора найдём
по теореме Пифагора найдём 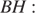

Ответ: 33.
29.  На отрезке
На отрезке  выбрана точка
выбрана точка  так, что
так, что  и
и  . Построена окружность с центром
. Построена окружность с центром 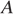 , проходящая через
, проходящая через  . Найдите длину отрезка касательной, проведённой из точки
. Найдите длину отрезка касательной, проведённой из точки 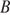 к этой окружности.
к этой окружности.
Решение.
 Проведём радиус
Проведём радиус  в точку касания. Из прямоугольного треугольника
в точку касания. Из прямоугольного треугольника  по теореме Пифагора найдём
по теореме Пифагора найдём 

Ответ: 11.
30.  На отрезке
На отрезке  выбрана точка
выбрана точка  так, что
так, что  и
и  . Построена окружность с центром
. Построена окружность с центром 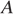 , проходящая через
, проходящая через  . Найдите длину отрезка касательной, проведённой из точки
. Найдите длину отрезка касательной, проведённой из точки 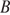 к этой окружности.
к этой окружности.
Решение.
 Проведём радиус
Проведём радиус 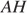 в точку касания. Из прямоугольного треугольника
в точку касания. Из прямоугольного треугольника 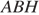 по теореме Пифагора найдём
по теореме Пифагора найдём 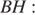

Ответ: 14.
31. 
Радиус окружности, вписанной в трапецию, равен 16. Найдите высоту этой трапеции.
Решение.
Радиус окружности, вписанной в трапецию, равен половине высоты трапеции. Поэтому высота равна 32.
Ответ: 32.
32. 
На окружности отмечены точки A и B так, что меньшая дуга AB равна 72°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Решение.
Пусть точка O — центр окружности. Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 72°. Треугольник AOB — равнобедренный. Значит,

Таким образом, поскольку угол OBC прямой, угол ABC равен 90° − 54° = 36°.
Ответ: 36.
 2020-05-25
2020-05-25 267
267








