2020-05-25
107
Пусть функция у = f (х) непрерывна на отрезке [ a, b ]. Как известно, такая функция на этом отрезке достигает наибольшего и наименьшего значений. Эти значения функция может принять либо во внутренней точке отрезка [ a, b ], либо на границе отрезка.
Для нахождения наибольшего и наименьшего значений функции на отрезке [ a, b ] необходимо:
1)найти критические точки функции в интервале (a, b);
2)вычислить значения функции в найденных критических точках;
3) вычислить значения функции на концах отрезка, то есть при x = а и х = b;
4)из всех вычисленных значений функции выбрать наибольшее и наименьшее.
Пример. Найти наибольшее и наименьшее значения функции
на отрезке [0; 3].
Находим критические точки:
Эти точки лежат внутри отрезка [0; 3]; y (1) = ‒ 3; y (2) = ‒ 4; y (0) = ‒ 8; y (3) = 1;
в точке x = 3 и 
в точке x = 0.
Исследование функции на выпуклость и точку перегиба.
Функция y = f (x) называется выпуклойвверх на промежутке (a, b), если ее график лежит под касательной, проведенной в любой точке этого промежутка, и называется выпуклой вниз (вогнутой), если ее график лежит над касательной.
Точка, при переходе через которую выпуклость сменяется вогнутостью или наоборот, называется точкой перегиба.
Алгоритм исследования на выпуклость и точку перегиба:
1. Найдем 
и критические точки второго рода, то есть точки в которых вторая производная равна нулю или не существует.
2. Нанести критические точки на числовую прямую, разбивая ее на промежутки. Найти знак второй производной на каждом промежутке; если 
, то функция выпуклая вверх, если 
, то функция выпуклая вниз.
3. Если при переходе через критическую точку второго рода поменяет знак и в этой точке вторая производная равна нулю, то эта точка ‒ абсцисса точки перегиба. Найти ее ординату 
.
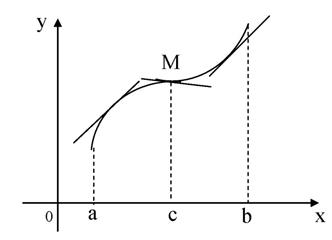
Рис.5
Рис. 6
