Асимптоты графика функции. Исследование функции на асимптоты

Определение. Асимптотой графика функции называется прямая, обладающая тем свойством, что расстояние от любой точки графика до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.

Рис. 7

Существуют три вида асимптот: вертикальные, горизонтальные и наклонные.

Определение. Прямая  называется вертикальной асимптотой графика функции у = f (х), если хотя бы один из односторонних пределов функции в этой точке равен бесконечности, то есть

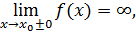
где  ‒ точка разрыва функции, то есть  не принадлежит области определения.

Пример.

D (y) = (‒ ∞; 2)  (2; + ∞)

x = 2 ‒ точка разрыва.

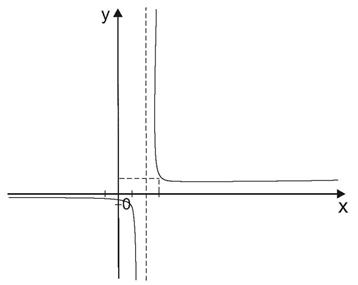
Определение. Прямая у = A называется горизонтальной асимптотой графика функции у = f(х) при , если

Пример.

x	0	3	1
y		1	‒ 1

Определение. Прямая у = kх + b (k ≠ 0) называется наклонной асимптотой графика функции у = f (х) при , где