2020-05-21
582
Если комплексному числу z = (cos φ + i sin φ), модуль которого равен 1, поставить в соответствие показательное выражение ei φ, то получим соотношение
cos φ + i sin φ = ei φ называется формулой Эйлера.
Любое комплексное число z можно записать в виде z = r ei φ
Эта форма записи комплексного числа называется показательной формой.
Действия над комплексными числами в тригонометрической форме:
1. 
2. z1/z2 = 
= 
3. zn = (r(cos j + i sin j))n = rn(cos nj + i sin nj)
4. 
= 
= 
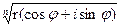, где k = 0, 1, 2, …, n-1
Последняя формула называется формулой Муавра.
Пример 2: z1 = 
(cos (- 
) + i sin (- )) и z2 = 2 (cos 
+ i sin )
= 
= 
(z2)3 = 23 (cos 3* + i sin 3* ) = 8 (cos 
+ i sin )
= 
= 
полагая k = 0, 1, 2, найдем
при к = 0
= 
= 
при к = 1
= 
= 
при к = 2
= 
= 
Действия над комплексными числами в показательной форме:
z1z2 = 
z1/z2 =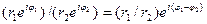 
zn =rn en i j
Пример 3: z1 = 
и z2 = 2 
z1z2 = 
z1/z2 =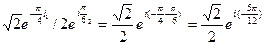 
(z2)3 = 23 
= 8 
