Тригонометрическая форма комплексного числа

Оглавление

 

Введение ………………………………………………………………………………… 3

 

 Лекция 1. Понятие о комплексных числах. Алгебраическая,

тригонометрическая, показательная формы записи комплексных

 чисел. Геометрическая интерпретация комплексных чисел.

Действия над комплексными числами. ……………………………………………… 3          

 Лекция 2. Матрицы. Определитель матрицы. Свойства определителей

 и их вычисление. Решение простейших матричных уравнений. Теорема Крамера.

Применение формул Крамера к решению систем линейных уравнений ……….. 8

 Лекция 3. Функции одной независимой переменной. Пределы.

Непрерывность функций. Производная, геометрический смысл.

Исследование функций. ………………………………………………………………. 11

Лекция 4. Неопределенный интеграл. Методы интегрирования.

Определенный интеграл. Вычисление определенного интеграла.

Геометрический смысл определенного интеграла. ……………………………….. 21

Лекция 5. Задачи, приводящие к дифференциальным уравнениям.

Дифференциальные уравнения с разделяющимися переменными. Общие и

частные решения. Однородные дифференциальные уравнения первого

порядка. Линейные однородные уравнения второго порядка с

постоянными коэффициентами. ……………………………………………………… 30

Лекция 6. Методы интегрирования. Метод прямоугольников. Метод трапеций.

Метод Симпсона. Абсолютная погрешность при численном

интегрировании ………………………………………………………………………. 35  

Лекция 7. Понятие о численном решении дифференциальных уравнений.

Формулы приближенного дифференцирования, основанные на

интерполяционных формулах Ньютона. Погрешности в определении

производной. Построение интегральной кривой. Метод Эйлера……………….. 40

Лекция 8-9. Числовые ряды. Сходимость и расходимость числовых рядов.

Признак сходимости Даламбера. Знакопеременные ряды. Абсолютная и

условная сходимость рядов. Интегральный признак Коши. Признак

Лейбница. Степенные ряды. Ряды Фурье …………………………………………… 60

Лекция 10. Понятие события и вероятности события. Достовернее и

невозможные события. Классическое определение вероятности. Теорема

сложения вероятностей. Применение теории вероятности при

решении профессиональных задач. ………………………………………………… 68

Лекция 11. Случайная величина. Дискретная и непрерывная случайные

величины. Закон распределения случайной величины…………………………… 74

Лекция 12. Математическое ожидание дискретной случайной величины.

Дисперсия случайной величины. Среднее квадратное отклонение

случайной величины………………………………………………………………….. 80

 

Литературные и интернет – источники …………………………………………….. 84

 

 

ВВЕДЕНИЕ

 

Конспект лекций составлен в соответствии с программой базового курса по математике для студентов 2 курса средних профессиональных учебных заведений, обучающихся по специальностям 150415 «Сварочное производство», 150402 «Металлургия цветных металлов», 270843 «Монтаж, наладка и эксплуатация электрооборудования промышленных и гражданских зданий» Он содержит как теоретическую часть, так и большое количество примеров и задач.

Основное назначение данного пособия состоит в том, чтобы помочь студенту преодолеть трудности при решении практических работ по математике.

При самостоятельном решении задач многие студенты нуждаются в постоянных консультациях относительно приемов и методов их решения. Такие консультации студент может получить при изучении этого пособия.

Такая форма изложение позволяет студенту сначала познакомиться с приемами решения типовых задач и оформлением записи их решений, а затем приступить к выработке навыков при решении практических работ.

Лекция 1. Понятие о комплексных числах. Алгебраическая, тригонометрическая, показательная формы записи комплексных чисел. Геометрическая интерпретация комплексных чисел. Действия над комплексными числами.

Понятие мнимой единицы Допустим, что существует такое число, квадрат которого равен – 1. Обозначим это число буквой i; тогда можно записать:

i ² = – 1.

Число i будем называть мнимой. Из этого равенства находим

Введение мнимой единицы позволяет нам теперь извлекать корни квадратные из отрицательных чисел.

Например,

 Символ a + bi называют комплексным числом с действительной частью a и мнимой частью bi, где a и b – действительные числа, b – коэффициент мнимой части.

Например, комплексное число 2 + 3i имеет действительную часть –  действительное число 2 и мнимую часть 3i, действительное число 3 – коэффициент мнимой части.

Комплексное число 2 – 3i имеет действительную часть число 2, мнимую часть – 3i, число – 3 – коэффициент при мнимой части.

Два комплексных числа равны тогда и только тогда, когда равны их действительные части и равны коэффициенты мнимых частей, т.е., если

a + bi = c +di, то a = c, b = d.

  Геометрическая интерпретация комплексного числа     Комплексное число z = a + bi можно изобразить точкой Z плоскости с координатами (a; b) (рис.1).

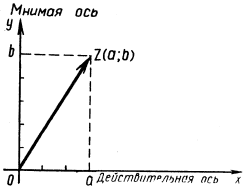
Рис.1

Для этого выберем на плоскости декартову прямоугольную систему координат. Действительные числа изображаются точками оси абсцисс, которую называют действительной (или вещественной) осью; чисто мнимые числа – точками оси ординат, которую будем называть мнимой осью.

Каждой точке плоскости с координатами (a; b) соответствует один и только один вектор с началом O (0; 0) и концом Z (a; b). Поэтому комплексное число z = a + bi можно изобразить в виде вектора с началом в точке O (0; 0) и концом в точке Z (a; b).

Пример 1. Изобразить на плоскости числа z ₁ = 5; z ₂ = – 3 i; z ₃ = 3 + 2 i; z ₄ = 5 – 2 i; z ₅ = – 3 + 2 i; z ₆ = – 1 – 5 i.

Решение. Заданные числа изображены на рис. 2.

Рис. 2

Действие над комплексными числами a+bj и c+dj в алгебраической форме

1) Правило сложения и вычитания комплексных чисел.

(a + bi) + (c + di) = (a + c) + (b + d)i.

Например:

+ =

Вычитание комплексных чисел определяется как операция, обратная сложению, и выполняется по формуле:

(a + bi) – (c + di) = (a – c) + (b – d)i.

Например:

- =

2) Правило умножения комплексных чисел.

(a + bi)(c + di) = (aс + bd) + (ad + bc)i.

Из определений 4 и 5 следует, что операции сложения, вычитания и умножения над комплексными числами осуществляются так, как будто мы выполняем операции над многочленами, однако с условием, что i2 = – 1.

Действительно: (a + bi)(c + di) = ac + adi + bdi2 = (ac – bd) + (ad + bc)i.

Например, * =

В частности, при умножении двух комплексных чисел a + bi и a – bi, называемых сопряженными комплексными числами, в результате получается действительное число, равное сумме квадратов действительной части и коэффициента при мнимой части. Действительно:

(a + bi)(a – bi) = a² – abi + abi – b²i² = a² + b².

Произведение двух чисто мнимых чисел – действительное число.

Например: 5i•3i = 15i² = – 15.

3) Деление комплексного числа a + bi на комплексное число c + di определяется как операция обратная умножению и выполняется по формуле:

.

Формула теряет смысл, если c + di = 0, так как тогда c² + d² = 0, т. е. деление на нуль и во множестве комплексных чисел исключается.

Обычно деление комплексных чисел выполняют путем умножения делимого и делителя на число, сопряженное делителю.

Например,

 

Тригонометрическая форма комплексного числа

Пусть комплексное число z = a + bi изображено в виде вектора с началом в точке O (0; 0) и концом Z (a; b) рис. 3 Определение 3. Модулем комплексного числа z = a + bi называется длина вектора, которую можно найти по формуле Обозначив модуль комплексного числа буквой r.

Рис. 3

Определение 4. Аргументом комплексного числа называется угол φ, который образует вектор с положительным направлением оси абсцисс. Величину угла φ можно найти с помощью формул:

z = r (cos φ + i sin φ)  называется тригонометрической формой комплексного числа.

Сформулируем правило перехода от алгебраической формы комплексного числа к тригонометрической.

1. Находят модуль комплексного числа r, для чего используют формулу

2. Для нахождения φ сначала определяют геометрически, в какой четверти находится точка z.

3. Составляют уравнения и и по решению одного из них находят угол φ.

4. Записывают комплексное число z в тригонометрической форме.