x2 = – 1.
Покажем, что расширив поле действительных чисел до поля комплексных чисел, мы получили поле, в котором каждое квадратное уравнение разрешимо, т.е. имеет решение. Так, уравнение x2 = – 1 имеет два решения: x1 = i, x2 = – i.
ПРИМЕР: Решите уравнение x2 – 4x + 5 = 0.
Решение. D = 16 – 4•1•5 = – 4 < 0, уравнение имеет мнимые корни: 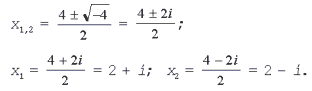
Лекция 2. Матрицы. Определитель матрицы. Свойства определителей и их вычисление. Решение простейших матричных уравнений. Теорема Крамера. Применение формул Крамера к решению систем линейных уравнений
Теорема. Система n уравнений с n неизвестными, определитель которой отличен от нуля, всегда имеет решение и притом единственное. Оно находится следующим образом: значение каждого из неизвестных равно дроби, знаменателем которой является определитель системы, а числитель получается из определителя системы заменой столбца коэффициентов при искомом неизвестном на столбец свободных членов.
Пусть дана система n линейных уравнений с n переменными:
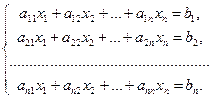
Из коэффициентов при неизвестных составим матрицу А, а из свободных членов — матрицу-столбец В, т. е.
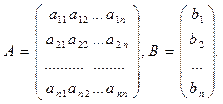
Определитель матрицы А обозначим ∆ и назовем определителем системы. Таким образом,
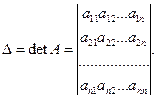
Пусть ∆ ≠ 0. Если в определителе системы заменить поочередно столбцы коэффициентов при 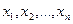 на столбец свободных членов, то получим n определителей (для n неизвестных)
на столбец свободных членов, то получим n определителей (для n неизвестных)
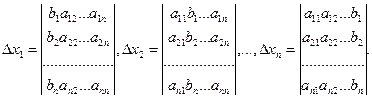
Тогда формулы Крамера для решения системы n линейных уравнений с n неизвестными запишутся так:
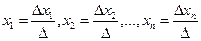
или короче
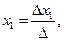 где
где 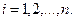
Рассмотрим случай, когда определитель системы равен нулю. Здесь возможны два варианта:
1. 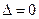 и каждый определитель
и каждый определитель 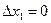 . Это имеет место только тогда, когда коэффициенты при неизвестных
. Это имеет место только тогда, когда коэффициенты при неизвестных 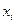 пропорциональны, т. е. каждое уравнение системы получается из первого уравнения умножением обеих его частей на число k. Очевидно, что при этом система имеет бесчисленное множество решений.
пропорциональны, т. е. каждое уравнение системы получается из первого уравнения умножением обеих его частей на число k. Очевидно, что при этом система имеет бесчисленное множество решений.
2. 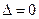 и хотя бы один из определителей
и хотя бы один из определителей 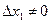 . Это имеет место только тогда, когда коэффициенты при всех неизвестных, кроме
. Это имеет место только тогда, когда коэффициенты при всех неизвестных, кроме 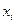 , пропорциональны. При этом получается система из противоречивых уравнений, которая не имеет решений.
, пропорциональны. При этом получается система из противоречивых уравнений, которая не имеет решений.
Пример 1. Решить систему уравнений
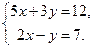
Решение. Вычислим определитель системы ∆ и определители 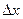 и
и 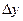 :
:
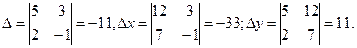
Найдем значения х и у по формулам Крамера:
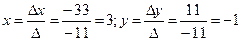
Итак, решение системы есть (3; —1).
Пример 2. Решить систему уравнений
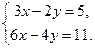
Решение. Вычислим определитель системы ∆ и определители 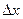 и
и 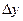 :
:
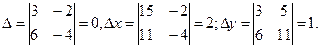
Так как 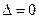 , а
, а 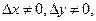 то система не имеет решений (уравнения противоречивы).
то система не имеет решений (уравнения противоречивы).
Пример 3. Решить систему уравнений
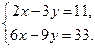
Решение. Вычислим определитель системы ∆ и определители 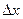 и
и 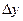 :
:
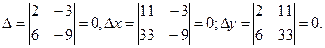
Данная система имеет бесчисленное множество решений (коэффициенты при неизвестных пропорциональны).
Пример 4. Решить систему уравнений
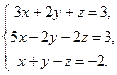
Решение. Вычислим определитель системы и определители при неизвестных:
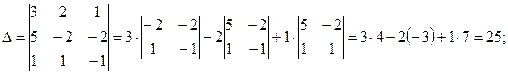
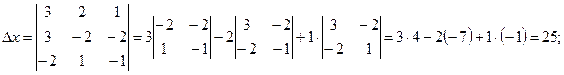
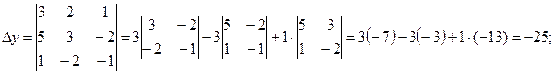
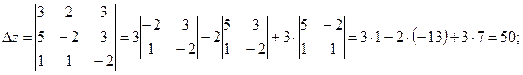
Найдем значения x, y, z по формулам Крамера:
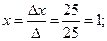
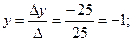
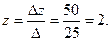
Ответ: (1; -1; 2).
Лекция 3. Функции одной независимой переменной. Пределы. Непрерывность функций. Производная, геометрический смысл. Исследование функций.
Предел функции.
Пусть функция y=f(x) определена в некоторой окрестности точки x0, кроме, быть может, самой точки x0.
О (на «языке последовательностей», или по Гейне): Число А называется пределом функции y=f(x) в точке x0, если для любой последовательности допустимых значений аргумента xn, nÎN (xn¹x0), сходящейся к x0 (т.е. 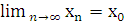 ), последовательность соответствующих значений f(xn),nÎN, сходитьсяк числу А.
), последовательность соответствующих значений f(xn),nÎN, сходитьсяк числу А.
Техника вычисления пределов.
При вычисление предела элементарной функции f(x) приходиться сталкиваться с двумя различными типами примеров.
1. Функция f(x) определена в предельной точке х = а. Тогда 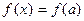
2. Функция f(x) в предельной точке х = а не определена или же вычисляется предел функции при х ® ¥. Тогда вычисление предела требует в каждом случае индивидуального подхода. В одних случаях (наиболее простых) вопрос сводиться непосредственно к применению теорем о свойствах бесконечно больших и бесконечно малых функций и связи между ними.
Более сложными случаями нахождения предела являются такие, когда функция f(x) в точке х = а или при х ® ¥ представляет собой неопределенность (типа 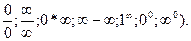
Приведем основные теоремы, на которых основано вычисление пределов.
1) Если существуют 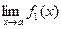 и
и 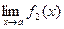 , то
, то
· 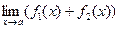 =
= 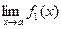 +
+ 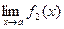
· 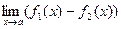 =
= 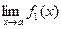 -
- 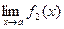
· 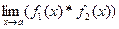 =
= 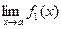 *
* 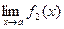
· 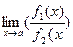 =
= 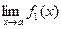 /
/ 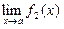 при
при 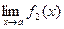 ¹ 0
¹ 0
2) 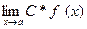 = С*
= С* 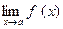 , где С – некоторое число
, где С – некоторое число
3) Связь между бесконечно малой и бесконечно большой величинами (С– некоторое число): 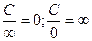
Рассмотрим некоторые ПРИМЕРЫ:
Пример 1. Найти предел функции 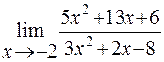
Решение: Имеем неопределенность вида 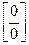 . Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель
. Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель 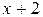 , который при
, который при 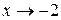 не равен нулю. В результате неопределенность будет раскрыта.
не равен нулю. В результате неопределенность будет раскрыта.
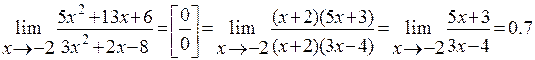
Пример 2. Найти предел функции 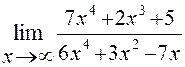
Решение: Имеем неопределенность вида 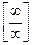 . Для ее раскрытия можно либо разделить числитель и знаменатель на наибольшую степень переменной x и учитывая, что величина обратная бесконечно большой величине есть бесконечно малая величина, раскроем исходную неопределенность, либо вынести переменную в наибольшей степени в числители и знаменатели дроби и сократить на наибольшую степень.
. Для ее раскрытия можно либо разделить числитель и знаменатель на наибольшую степень переменной x и учитывая, что величина обратная бесконечно большой величине есть бесконечно малая величина, раскроем исходную неопределенность, либо вынести переменную в наибольшей степени в числители и знаменатели дроби и сократить на наибольшую степень.
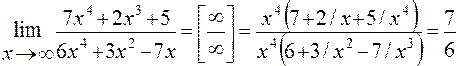
Пример 3. Найти предел функции 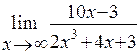
Решение: Имеем неопределенность вида 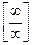 . Раскрываем ее аналогично тому как это сделано в примере 2.
. Раскрываем ее аналогично тому как это сделано в примере 2.
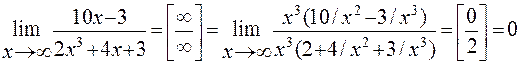
Пример 4. Найти предел функции 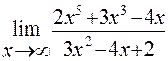
Решение: Имеем неопределенность вида 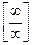 . Раскрываем ее аналогично тому как это сделано в примере 2.
. Раскрываем ее аналогично тому как это сделано в примере 2.
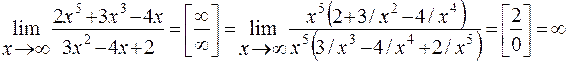
Пример 5. Найти предел функции 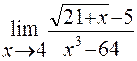
Решение: Имеем неопределенность вида 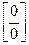 . Для ее раскрытия умножим числитель и знаменатель на выражение сопряженное числителю, разложим выражение стоящее в знаменателе на множители по формуле разности кубов и сократим числитель и знаменатель на общий множитель
. Для ее раскрытия умножим числитель и знаменатель на выражение сопряженное числителю, разложим выражение стоящее в знаменателе на множители по формуле разности кубов и сократим числитель и знаменатель на общий множитель 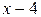 , который при
, который при 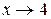 не равен нулю. В результате неопределенность будет раскрыта.
не равен нулю. В результате неопределенность будет раскрыта.
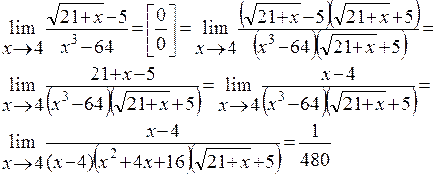
Вычисление пределов с использованием замечательных пределов.
Применение замечательных пределов
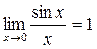 и
и 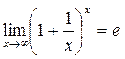
Пользуясь этими формулами, можно вычислить ряд пределов.
Пример 6. Вычислить 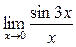 .
.
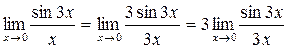 , заменяя 3x = y и учитывая, что y → 0 при x → 0, получаем:
, заменяя 3x = y и учитывая, что y → 0 при x → 0, получаем:
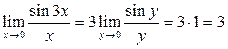 .
.
Пример 7. Вычислить 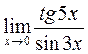
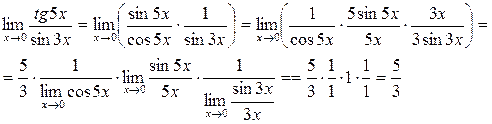
Здесь мы воспользовались известным из курса средней школы пределом:
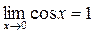 .
.
Пример 8. Вычислить 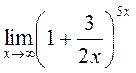
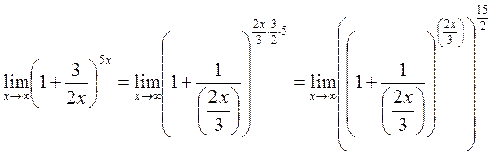
Заменяя 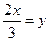 и учитывая, что y → ∞ при x → ∞, можем написать:
и учитывая, что y → ∞ при x → ∞, можем написать:
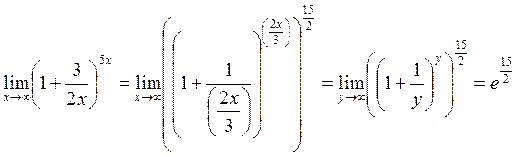 .
.
 2020-05-21
2020-05-21 160
160








