Задание 6. Максимальное значение скорости частицы, совершающей гармонические колебания, согласно уравнению x (t) = 0,02 cos (5 t – π /4), м, равно, в метрах в секунду (м/с),
1) 0,01; 2) 0,02; 3) 0,04; 4) 0,08; 5) 0,1.
Дано:
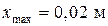
 = 5 с-1
Найти: = 5 с-1
Найти: 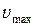 -? -?
| Решение. Согласно определению скорость частицы, совершающей гармонические колебания, равна производной по времени от координаты x и задается уравнением:
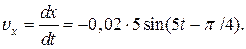 Максимальной скорость будет при максимальном значении синуса, равном 1. Следовательно, максимальное значение скорости частицы
Максимальной скорость будет при максимальном значении синуса, равном 1. Следовательно, максимальное значение скорости частицы
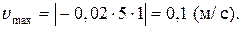 Номер правильного ответа: 5.
Номер правильного ответа: 5.
|
Задание 7. При гармонических электрических колебаниях в колеба-тельном контуре максимальное значение энергии электрического поля конденсатора равно 50 Дж, максимальное значение энергии магнитного поля катушки 50 Дж. Как изменяется во времени полная энергия электромагнитного поля контура?
1) От 0 до 50 Дж. 2) От 0 до 100 Дж.
3) Не изменяется и равна 50 Дж. 4) Не изменяется и равна 100 Дж.
5) От 50 до 100 Дж.
| Дано: We max = 50 Дж Wm max = 50 Дж Найти: ∆W -? | Решение. Энергия колебаний в колебательном контуре складывается из энергии электрического поля заряженного конденсатора и энергии магнитного поля тока в катушке. С течением времени эта энергия остается неизменной, причем в те моменты времени, когда энергия электрического поля дос-тигает своего максимального значения (50 Дж), энергия магнитного поля оказывается равной нулю, и наоборот. Следовательно, полная энергия электромагнитного поля контура не изменяется и равна 50 Дж. Номер правильного ответа: 3. |
Задание 8. Дифференциальное уравнение затухающих колебаний имеет вид: 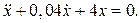 Среди приведенных утверждений укажите верное.
Среди приведенных утверждений укажите верное.
1) Собственная циклическая частота гармонических колебаний равна 2 рад/с.
2) Циклическая частота затухающих колебаний равна 4 рад/с.
3) Коэффициент затухания равен 0,04 с – 1.
4) Частота затухающих колебаний равна 2 Гц.
5) Период затухающих колебаний равен 4 с.
Дано: 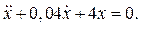 Найти:
Найти: 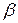 , , 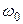 -? -?
| Решение. Дифференциальное уравнение затухающих колебаний имеет вид
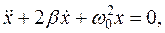 где
где  – коэффициент затухания; – коэффициент затухания;
 – частота собственных колебаний. – частота собственных колебаний.
|
Сравнивая коэффициенты, стоящие при 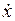 и x, видим:
и x, видим:
2 β = 0,04; 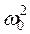 = 4 (без единиц измерения).
= 4 (без единиц измерения).
Таким образом, коэффициент затухания β = 0,02 с – 1, собственная циклическая частота гармонических колебаний 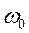 = 2 рад/с.
= 2 рад/с.
Номер правильного ответа: 1.
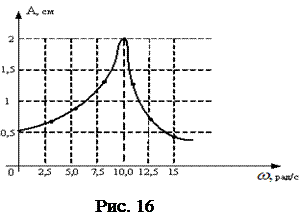
Задание 9. На рис. 16 представ-лена зависимость амплитуды вынужден-ных колебаний математического маятни-ка от циклической частоты внешней силы при слабом затухании. Длина нити маятника в сантиметрах равна (g = 10м/с2)
1) 100; 2) 50; 3) 20; 4) 14; 5) 10.
Дано:
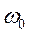 = 10 рад/с
Найти: = 10 рад/с
Найти: 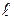 -? -?
| Решение. Из рис. 16 видно, что резонанс амплитуды колебаний происходит при циклической частоте, равной 10 рад/с. В случае слабого затухания резонансная частота совпадает с собственной частотой колебаний математи-ческого маятника, которая определяется по формуле:
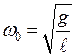 . .
|
Выразим из этой формулы длину нити 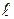 и, приняв
и, приняв 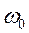 = 10 рад/с, получим:
= 10 рад/с, получим:
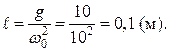
Таким образом, длина нити математического маятника равна 10 см.
Номер правильного ответа: 5.
Задание 10. Если в упругой среде распространяется волна со скоростью 6 м/с и периодом колебаний 0,5 с, то минимальное расстояние между двумя частицами среды, фазы колебаний которых отличаются на 2 π, равно
1) 1,5 м; 2) 3 м; 3) 4 м; 3) 6 м; 5) 12 м.
Дано:
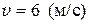
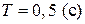 Найти:
Найти: 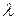 -? -?
| Решение. Минимальное расстояние между двумя частицами среды, фазы колебаний которых отличаются на 2π, называется длиной волны и равно:
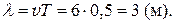
|
Номер правильного ответа: 2.
 2020-05-21
2020-05-21 568
568








