Вычисление перемещений методом Мора

Метод начальных параметров

Для углов поворота

(6)

Для прогибов:

(7)

где θ – угол поворота сечения; w – прогиб; θo – угол поворота в начале координат; w0 – прогиб в начале координат; dі – расстояние от начало координат до i-й опоры балки; ai – расстояние от начало координат до точки приложения сосредоточенного момента Mi; bi – расстояние от начало координат до точки приложения сосредоточенной силы Fi; сi – расстояние от начало координат до начала участка распределенной нагрузки qi; Ri и Мрi – реакция и реактивный момент в опорах балки.

Определение стрелы прогибов для простых случаев

Рис. 3. Примеры нагрузок балок

Вычисление перемещений методом Мора

Если не требуется знание уравнения изогнутой линии бруса, а необходимо определить только линейные или угловые перемещения отдельного сечения, удобнее всего воспользоваться методом Мора.Для балок и плоских рам интеграл Мора имеет вид:

где δ – искомое перемещение (линейное или угловое); М_p, М_i– аналитические выражения изгибающих моментов соответственно от заданной и единичной cилы; EJ_x – жесткость сечения балки в плоскости изгиба. При определении перемещений нужно рассматривать два состояния системы: 1 – действительное состояние, с приложенной внешней нагрузкой; 2 – вспомогательное состояние, в котором балка освобождается от внешней нагрузки, а к сечению, перемещение которого определяется, прикладывается единичная сила, если определяется линейное перемещение, или единичный момент, если определяется угловое перемещение (рис.5).

а б

Рис. 5. Определение перемещений:
а – действительное состояние; б, в – вспомогательные состояния

Формулу Мора можно получить, например. используя принцип возможных перемещений.

а б

Рис.6. Схема рамы:
а – под воздействием силы; б – внутренние усилия

Рассмотрим схему (рис. 6а), когда в точке А в направлении искомого перемещения ΔA приложена единичная сила , вызывающая в поперечном сечении системы внутренние силовые факторы 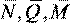(рис. 6, б). В соответствии с принципом возможных перемещений работа этих внутренних силовых факторов на любых возможных перемещениях должна равняться работе единичной силы на возможном перемещении δΔA:

Выбираем возможные перемещения пропорциональными действительным:

И после подстановки получим:

При учете, что

приходим к формуле Мора

(8)

которая служит для определения любых обобщённых перемещений в стержневых системах.

В случае, когда брус работает только на изгиб (Mx ≠ 0, Nz = Mz = My = Qx = Qy = 0), выражение (1) принимает вид:

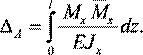(9)

Правило Верещагина позволяет заменить непосредственное интегрирование в формулах Мора так называемым перемножением эпюр. Способ вычисления интеграла Мора путем замены непосредственного интегрирования перемножением соответствующих эпюр называется способом (или правилом) Верещагина, заключающемся в следующем: чтобы перемножить две эпюры, из которых хотя бы одна является прямолинейной, нужно площадь одной эпюры умножить на ординату другой эпюры, расположенную под центром тяжести первой (ординаты используются только с прямолинейных эпюр). Эпюры сложного очертания могут быть разбиты на ряд простейших: прямоугольник, треугольник, квадратичную параболу и т.п. (рис. 7).

Рис. 7. Простейшие эпюры

Справедливость правила Верещагина.

Рис. 8. Схема перемножения эпюр:
а – произвольная эпюра; б – прямолинейная

Приведены две эпюры изгибающих моментов, из которых одна Мk имеет произвольное очертание, а другая Мi прямолинейна (рис. 8). Сечение стержня считаем постоянным. В этом случае

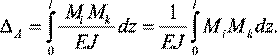
Величина Mkdz представляет собой элементарную площадь dω эпюры Мk (заштрихована). Получаем

Но Mi = ztg α, поэтому,

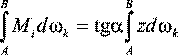
Выражение представляет собой статический момент площади эпюры Мk относительно оси у, проходящей через точку О, равный ωkΖc, где ωk – площадь эпюры моментов; Ζс – расстояние от оси у до центра тяжести эпюры М_k. Из рисунка очевидно:

Ζ_c= М_i/tg α,

где Мi – ордината эпюры Mi, расположенная под центром тяжести эпюры Мk (под точкой С).

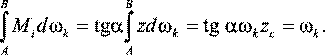(10)

Формула (10) представляет правило вычисления интеграла Мора: интеграл равен произведению площади криволинейной эпюры на ординату, взятую с прямолинейной эпюры и расположенную под центром тяжести криволинейной эпюры.

Встречающиеся на практике криволинейные эпюры могут быть разбиты на ряд простейших: прямоугольник, треугольник, симметричную квадратичную параболу и т.п.

При помощи разбивания эпюр на части можно добиться того, что при перемножении все эпюры были бы простой структуры.

Пример вычисления перемещений. Требуется определить прогиб в середине пролета и угол поворота левого опорного сечения балки, нагруженной равномерно распределенной нагрузкой (рис. 36, а), способом Мора-Верещагина.

Рассмотрим 3 состояния балки: грузовое состояние (при действии распределенной нагрузки q;) ему соответствует эпюра Mq (рис. 9, б), и два единичных: при действии силы , приложенной в точке С (эпюра , рис. 9, в), и момента , приложенного в точке В (эпюра , рис. 9, г).

Прогиб балки в середине пролета:

Обратим внимание, что перемножение эпюр выполняется для половины балки, а затем из-за симметрии) полученный результат удваивается. При вычислении угла поворота сечения в точке В площадь эпюры Mq умножается на расположенную под ее центром тяжести ординату эпюры (1/2, рис. 9, г), т.к. эпюра изменяется по прямой линии: