Тема «Уравнение касательной»

    Прямая называется касательной к графику функции, если она имеет одну общую точку с графиком функции и не пересекает его.

    Общий вид уравнения прямой .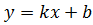

 

Алгоритм написания уравнения касательной.

1)Записать общий вид уравнения касательной

2)Вычислить значение функции в точке .

3)Найти производную от данной функции.

4)Вычислить значение производной в точке .

5)Полученные значения в пунктах 2 и 4 подставить в пункт 1.

 

Примеры выполнения заданий

Написать уравнение касательной к графику функции

в точке .

1)

2)

    =

3)

4)

5)

 

Задания для самостоятельной работы

Написать уравнение касательной к графикам функций

в точке .

в точке .

в точке .

в точке .

 

Тема «Наибольшее и наименьшее значения функции»

Алгоритм нахождения наибольшего и наименьшего значений функции.

1) Найти производную от данной функции

2) Приравнять производную к нулю и найти корни

3) Проверить попадают ли полученные корни в данный интервал

4) Подставить все значения, входящие в интервал, в функцию и вычислить

5) Из полученных значений выберем наибольшее и наименьшее значения функции.

Примеры выполнения заданий

    Найдите наибольшее и наименьшее значения функции  на интервале [ - 1; 6].

1)

2)

     

3)

         -1   0              4       6

4)

5) 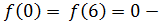наименьшее значение функции

 - наибольшее значение функции.

 

    Задания для самостоятельной работы

 1)Найдите наибольшее и наименьшее значения функции 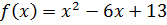 на интервале [ -0; 6].

     2) [ 0; 3].

     3) [ - 4; 4].

 

Лекции переписываем в тетрадь.

Все решения выполняем в тетрадях, фотографируем и присылаем в вк (до 10.04.2020