Угловая дисперсия
Одной из главных характеристик спектрального прибора является угловая дисперсия. По определению, угловой дисперсией  называется величина:
называется величина:
 (22)
(22)
Здесь и далее  – знак дифференциала, так как буква
– знак дифференциала, так как буква  используется – она обозначает постоянную решетки.
используется – она обозначает постоянную решетки.
В определении угловой дисперсии 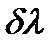 – разность длин волн двух соседних линий,
– разность длин волн двух соседних линий,  – соответствующая разность углов, под которыми наблюдаются главные максимумы. Выразим угловую дисперсию через постоянную решетки
– соответствующая разность углов, под которыми наблюдаются главные максимумы. Выразим угловую дисперсию через постоянную решетки 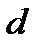 , порядок спектра
, порядок спектра  и угол
и угол  , под которым наблюдается максимум. Для этого найдем дифференциал от правой и левой части условия главного максимума:
, под которым наблюдается максимум. Для этого найдем дифференциал от правой и левой части условия главного максимума:
 , (23)
, (23)
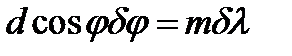 , (24)
, (24)
 (25)
(25)
Угловая дисперсия принимает только положительные значения. Угловая дисперсия тем больше, чем меньше период решетки, она растет с ростом порядка максимума. Угловая дисперсия одинакова в максимумах с порядками 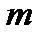 и
и  . При малых
. При малых  :
:  и
и  .
.

Рис. 13. К определению угловой дисперсии
Разрешающая сила дифракционной решетки
Разрешающая сила дифракционной решетки определяется следующим образом:
 (26)
(26)
Здесь  – минимальная разница в длинах волн соседних спектральных линий, при которой эти линии еще можно наблюдать раздельно.
– минимальная разница в длинах волн соседних спектральных линий, при которой эти линии еще можно наблюдать раздельно.
Критерий Релея
Критерий Релея определяет величину  в соответствии с рис.14. Считают, что линии разрешены, если главный максимум линии
в соответствии с рис.14. Считают, что линии разрешены, если главный максимум линии  и добавочный минимум линии
и добавочный минимум линии  совпадает, следовательно:
совпадает, следовательно:
 (27)
(27)
 (28)
(28)
 (29)
(29)
По определению разрешающая сила:
 (30)
(30)
 В результате получим:
В результате получим:
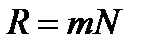 (31)
(31)
Рис. 14.Критерий Релея
Разрешающая сила R есть величина, обратная относительной погрешности определения длины волны. Она показывает, во сколько раз длина волны  больше минимально возможной абсолютной погрешности
больше минимально возможной абсолютной погрешности  .
.
Подчеркнем, что 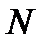 в формуле для разрешающей силы – это число щелей, принимающих участие в образовании главного максимума порядка
в формуле для разрешающей силы – это число щелей, принимающих участие в образовании главного максимума порядка  . Если поперечный размер падающего на решетку пучка света
. Если поперечный размер падающего на решетку пучка света  больше длины решетки
больше длины решетки  , то
, то  , где
, где  – постоянная решетки.
– постоянная решетки.

Рис.15. Поперечные размеры пучка и решетки
Если же 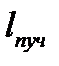 <
<  , то
, то 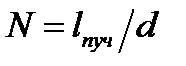
Кроме того, предполагается, что колебания от всех 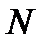 щелей когерентны.
щелей когерентны.
 2020-06-12
2020-06-12 145
145








