Оценка сложности и памяти

Для некоторой величины, зависящей от переменного x, известны её значения в n + 1 точках. Задача заключается в поиске многочлена степени m

(m < n + 1), наиболее точно аппроксимирующего данную величину. Эту задачу можно решить, построив конечное число многочленов Фурье и найдя коэффициенты, соответствующие каждому из них. Алгоритм, реализующий данную процедуру, я назову FourierPolinoms (от «Fourier» - Фурье, «polinom» - многочлен). FourierPolinoms получает на вход n пар действительных чисел вида (x_i, y_i), а также натуральное число m – степень аппроксимирующего многочлена. Алгоритм строит m + 1 многочленов Фурье степеней от 0 до m.

Каждый многочлен однозначно определяется своими коэффициентами. Поэтому под построением многочлена степени d удобно понимать задание вектора из пространства вектор-строк длины d + 1 над полем действительных чисел, в котором каждое число является коэффициентом при соответствующем одночлене строящегося многочлена. При этом построение системы из l многочленов сводится к построению матрицы M размеров l x (r + 1), где r – степень многочлена наибольшей степени системы. Далее для определённости буду считать, что элемент i -ой строки j -го столбца матрицы M есть коэффициент i -го многочлена из системы многочленов, стоящий перед одночленом степени j – 1.

В случае построения системы многочленов Фурье строится матрица Q размеров (m + 1) x (m + 1). Построением такой матрицы и занимается FourierPolinoms. Для её хранения требуется (m + 1) x (m + 1) ячеек памяти.

Замечание: учитывая структуру системы многочленов Фурье и способ хранения многочленов, описанный в конце предыдущего абзаца, матрица Q имеет нижнетреугольный вид, то есть почти наполовину заполнена нулями. Это обстоятельство резонно использовать при оптимизации части алгоритма, отвечающей за память.

Алгоритм вычисляет матрицу Q последовательно, используя следующие формулы:

q₀(x) = 1                                                                                                            (1),

q₁(x) = x -                                                                                        (2),

a_{k + 1} =                                                                                               (3),

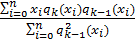b_k =                                                                       (4),

q_{k + 1}(x) = xq_k(x) - a_{k + 1}q_k(x) - b_k q_{k - 1}(x)                                                             (5),

для каждого k от 1 до m – 1.

После вычисления матрицы Q FourierPolinoms считает вектор коэффициентов , опираясь на формулу

c_j =                                                                                                 (6), где j меняется от 1 до m.

Вектор коэффициентов аппроксимирующего многочлена получается умножением вектора коэффициентов  на матрицу Q, и служит выходом алгоритма FourierPolinoms.

Вычислять сложность FourierPolinoms буду в терминах «О» больших, дабы избежать громоздких записей, которые в конце концов всё равно были бы упрощены до асимптотических зависимостей.

Действие (1) – просто запись числа в левый верхний элемент матрицы Q, требующая О(1) операций.

Действие (2) требует подсчёта суммы элементов сложности О(n) (x_i суммируются n раз), деления на константу и записи двух результатов в матрицу Q сложности О(1).

Вычисления (3) и (4) используют расчёт значения многочлена k -ой степени в точке. Посчитаю её.

p(a) = p₀ + p₁a + p₂a² + … + p_ka^k – формула для расчёта значений многочлена p в точке a. Каждый одночлен i -ой степени вычисляется со сложностью О(i) – необходимо умножить нa само на себя i – 1 раз, а затем на коэффициент p_i при одночлене. Многочлен образуют k + 1 одночленов, для вычисления каждого требуется сложность O(i) (где i меняется от 0 до k), как было выяснено только что. Одночлен нулевой степени требует 0 операций, одночлен первой степени – 1 операцию, одночлен второй степени – 2 операции и так далее, вплоть до одночлена k-ой степени. Тогда вычисление всех k + 1 одночленов требует О(0 + 1 + 2 + … + k) = O( ) = O(k²) операций. Наконец, для вычисления значения многочлена p в точке a требуется сложить вычисленные значения одночленов, это действие прибавляет к сложности k операций. Но на асимптотике это не сказывается: О(k² + k) = O(k²).

Вернусь к вычислению сложности действия (3). Расчёт числителя требует сложения n произведений. Каждое произведение требует О(2k² + 2) = О(k²) операций. Тогда расчёт числителя требует всего О(nk²) операций. Расч ёт знаменателя требует сложения n произведений, каждое из которых требует О(2k² + 1) операций. Тогда расчёт знаменателя подобно расчёту числителя требует О(nk²) операций. Вычисление каждого коэффициента из формулы (3) предполагает деление двух вычисленных значений сложности 1. Итак, итоговая сложность вычисления действия (3): О(2nk² + 1) = О(nk²). Коэффициент а_k алгоритм считает m – 1 раз со сложностью, посчитанной выше для каждого k (для k от 1 до m - 1). Хранение занимает m + 1 ячеек памяти. Теперь о сложности: О( ) = О( ) = O(nm³) = O(n⁴). Последнее равенство справедливо согласно начальному условию работы алгоритма: m < n + 1.

Анализ сложности вычисления коэффициентов b_k из формулы (4) аналогичен вышеприведённому анализу для коэффициентов a_k из формулы (3), и ответ получается тот же: O(n⁴). Для хранения всех коэффициентов b_k тоже требуется m + 1 ячеек памяти.

В связи с вышеуказанным соответствием между матрицами и системами многочленов формулу (5) можно переписать на языке матриц:

Q_{k + 1, j} = Q_{k, j – 1} – a_{k + 1}Q_{k, j} – b­_kQ_{k – 1, j}                                                      (7)

для всех j от 1 до m + 1 и для всех k от 1 до m – 1. Матрица Q содержит

(m + 1)² элементов. Тогда её расчёт требует О(m²h) операций, где h – сложность расчёта каждой ячейки матрицы Q. Займусь поиском h. Формула (7) говорит о том, что каждая ячейка матрицы получается при помощи двух умножений и двух вычитаний вычисленных ранее констант – элементов той же матрицы Q и хранящихся в памяти коэффициентов a_k и b_k. То есть сложность этого действия h = О(4) = О(1). Итак, сложность расчёта матрицы Q составила О(m²).

Найду теперь сложность вычисления и требуемую память для вектора коэффициентов . Сложность расчёта значения многочлена степени j в точке была получена ранее – О(j²). Числитель формулы (6) получается путём сложения n элементарных произведений, каждое из которых считается со сложностью О(1), что можно сказать и о знаменателе. Тогда сложность расчёта числителя, как и знаменателя, составляет О(nj²). Деление числителя на знаменатель стоит 1 единицу сложности, значит каждый коэффициент c_j считается со сложностью О(nj²). Но j пробегает все натуральные значения от 1 до m, и сложность вычисления вектора коэффициентов  составляет О( ) = O(nm³) = O(n⁴). А для его хранения требуется m + 1 ячеек памяти.

Последний шаг алгоритма – получение вектора коэффициентов аппроксимирующего многочлена путём умножения вектора коэффициентов

на матрицу Q. Каждый из m + 1 коэффициентов аппроксимирующего многочлена считается путём умножения  на соответствующий вектор-столбец матрицы Q. Сложность умножения вектор-строки на вектор-столбец длины m + 1 есть О(m) – при этом происходит m элементарных операций умножения и m элементарных операций сложения. В связи с этим искомая сложность умножения  на матрицу Q составляет О(m²).

Соединяя вычисленные на каждом этапе работы алгоритма FourierPolinoms сложности, можно заключить, что его сложность составляет О(n⁴), наиболее сложные процедуры – вычисление коэффициентов векторов коэффициентов a_k, b_k, c_k.

Используемые ячейки памяти:

Матрица Q: (m + 1)².

Вектор  (из коэффициентов a_k): m + 1.

Вектор  (из коэффициентов b_k): m + 1.

Вектор : m + 1.

Итого: m² + 5m + 4 = (m + 4)(m + 1) = O(m²).

Алгоритм прямоугольников-трапеций (численное интегрирование)

 

Оценка сложности

Некоторая функция подвергается численному интегрированию на отрезке методом прямоугольников. Как работает этот метод? На вход алгоритма, который я обозначу RectangleAreaCalculating (от «rectangle» - прямоугольник, «area» - площадь, «calculating» - вычисление), подаётся четыре параметра: интегрируемая функция (f), левый конец отрезка (a), правый конец отрезка (b), погрешность (e). RectangleAreaCalculating разбивает отрезок [a; b] на [ ] равных подотрезков ([x] здесь обозначает целую часть вещественного числа x), и на каждом подотрезке выполняет однотипные действия: вычисляет значение функции f в середине подотрезка и умножает его на e – длину подотрезка. Все полученные произведения RectangleAreaCalculating суммирует, образуя на выходе приближённое значение интеграла, которое и служит выходом алгоритма.

Пусть [c; d] – подотрезок, образовавшийся в результате разбиения программой RectangleAreaCalculating отрезка [a; b]. Сложность вычисления середины подотрезка [c; d] - , составляет 2 единицы (1 – сложение c и d, 1 – деление результата на 2). Для дальнейшего анализа сделаю допущение: на всём отрезке [a; b] функция f вычисляется с одинаковой сложностью, которую я обозначу через C_f (от «complexity» - сложность), которая зависит от вида функции f. Действительно, например, функции f₁(x) = x­­­ ² и f₂(x) = 2  – 7 вычисляются с разной сложностью. Сложность умножения результата вычисления функции f на длину e подотрезка [c; d] составляет 1 единицу. Таким образом, сложность работы RectangleAreaCalculating на каждом подотрезке [c; d] есть 3 + C_f. Всего таких подотрезков [ ]. Резюмируя вышеизложенное, сложность вычисления приближённого значения интеграла методом прямоугольников равна

                                            [ ](3 + C_f)                                                    (8)

Пусть теперь та же самая функция f численно интегрируется на том же самом отрезке [a; b] методом трапеций. Входные данные алгоритма метода трапеций, который я обозначу через TrapezeAreaCalculating (от «trapeze» - трапеция, «area» - площадь, «calculating» - вычисление (хочется верить, последние два слова вызвали дежавю)), совпадают с входными данными RectangleAreaCalculating. И вообще, вплоть до разбиения отрезка [a; b] на подотрезки TrapezeAreaCalculating работает точно так же, как и RectangleAreaCalculating. Пусть [c; d] – подотрезок, образовавшийся в результате разбиения отрезка [a; b] программой TrapezeAreaCalculating. Метод трапеций требует вычисления значения функции f в точках c и d. Сложность такого вычисления – 2 C_f (напомню, C_f – сложность вычисления функции f в произвольной точке отрезка [a; b]). Далее по алгоритму результат делится на 2 и умножается на e. Эти две элементарные операции добавляют 2 единицы к уже полученной сложности. То есть сложность TrapezeAreaCalculating на каждом подотрезке [c; d] составляет 2 C_f + 2. На завершающем этапе TrapezeAreaCalculating суммирует промежуточные результаты работы, полученные на каждом подотрезке. А всего таких подотрезков [ ]. Таким образом, сложность вычисления приближённого значения интеграла методом трапеций равна

                                              [ ](2C_f + 2)                                                 (9).

Анализируя формулы (8) и (9), можно прийти к заключению, что сложность двух рассмотренных алгоритмов во многом зависит от сложности вычисления значений интегрируемой функции. Метод трапеций требует большего числа элементарных операций, чем метод прямоугольников, однако их асимптотика совпадает. Замечу, что полученные оценки верны для конкретной (простейшей) реализации исследуемых методов. Оптимизируя вычисления, можно добиться других результатов.