Пример решения задачи 1

Геометрия

7-Б класс 13.05.2020                                                              7-А класс 14.05.2020

Тема урока
Решение задач на применение признаков равенства треугольников.
Цели урока: -повторить и обобщить основные методы решения геометрических задач;

- совершенствовать навыки решения геометрических задачна применение признаков равенства треугольников;

Ознакомьтесь с теоретическим материалом и вспомните основные положения теории по теме урока.

         Теоретический материал для самостоятельного повторения.

Давайте вспомним, что мы уже знаем о треугольнике и также закрепим навыки решения задач на доказательство равенства треугольников, применения признаков равенства треугольников.

Рассмотрим ∆АВС

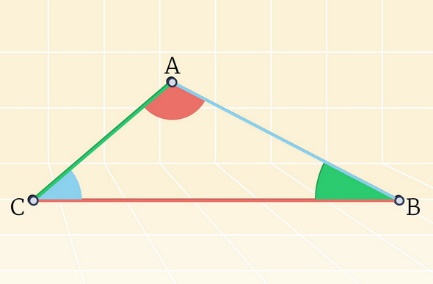
А, В, С – вершины треугольника АВС, АВ, ВС, СА – стороны треугольника АВС,

∠А, ∠В, ∠С – углы треугольника АВС

Сумма длин всех его сторон – периметр треугольника. Р = АВ + ВС + СА

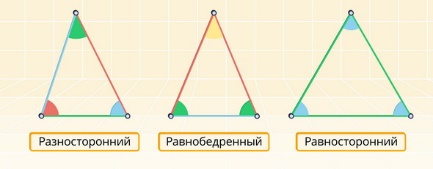
Вспомним виды треугольников.

Разносторонний треугольник – все его стороны имеют различную длину.

Равнобедренный треугольник – две его стороны равны между собой.

Равносторонний треугольник – все его стороны равны между собой.

Теперь повторим теоремы о равенстве треугольников: признаки равенства треугольников.

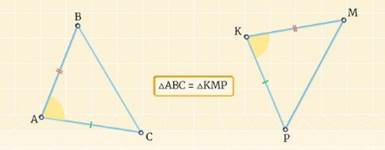
1) Первый признак равенства треугольников.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

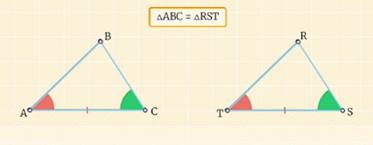
2) Второй признак равенства треугольников.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

3) Третий признак равенства треугольников.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Ознакомьтесь с примерами решения задач по теме урока.

Пример решения задачи 1

Докажите, что ∆ABC = ∆A₁B₁C₁, если AB = A₁B₁, AC = A₁C₁, AM = A₁M₁, при этом AM и A₁M₁ – медианы треугольников.

Дано:

∆ABC

∆A₁B₁C₁

AB = A₁B_1, AC = A₁C_1, AM = A₁M₁

AM и A₁M₁ – медианы треугольников

Доказать: ∆ABC = ∆A₁B₁C₁

Доказательство:

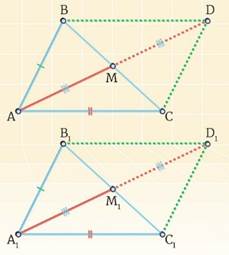
Построим AM = MD A₁M₁ = M₁D₁   Т. к. AM = A₁M₁ и AM = MD, A₁M₁ = M₁D₁ → MD = M₁D₁ → AD = A₁D₁

∆AMB = ∆DMC (по первому признаку равенства треугольников), т. к. BM = MC (AM – медиана), ∠BMA = ∠DMC (по свойству вертикальных углов), AM = MD (построение).

Аналогично: ∆A₁M₁B₁ = ∆D₁M₁C₁(1 признак равенства треугольников), т. к. B₁M₁ = M₁C₁ (A₁M₁ – медиана по условию), ∠B₁M₁A₁ = ∠D₁M₁C₁ (по свойству вертикальных углов), A₁M₁ = M₁D₁ (построение).

AB = DC = A₁B₁, A₁B₁ = D₁C₁→ DC = D₁C₁.

Аналогично: ∆AMC = ∆DMB (по первому признаку равенства треугольников), т. к. BM = MC (AM – медиана по условию), ∠BMD = ∠AMC (по свойству вертикальных углов)), AM = MD (построение).

∆A₁M₁C₁ = ∆D₁M₁B₁ (по первому признаку равенства треугольников), т. к. B₁M₁ = M₁C₁ (A₁M₁ – медиана по условию),

∠B₁M₁D₁ = ∠A₁M₁C₁ (по свойству вертикальных углов), A₁M₁ = M₁D₁ (построение).

BD = B₁D₁ = AC = A₁C₁→ ∆ABD = ∆A₁B₁D₁ (3 признак равенства треугольников) по трём равным сторонам. →∠BAM = ∠B₁A₁M₁

∆ACD = ∆A₁C₁D₁ (по третьему признаку равенства треугольников) → ∠CAM = ∠C₁A₁M_1.

→∠BAM + ∠CAM = ∠B₁A₁M₁ + ∠C₁A₁M₁ = ∠A = ∠A₁

→∆ABC = ∆A₁B₁C₁ (по первому признаку равенства треугольников), AB = A₁B₁, AC = A₁C₁, ∠A∠A₁.

Что и требовалось доказать.

Рассмотрим решение задачи на доказательства методом от противного.