2020-06-08
142
Для электрического поля в вакууме были выведены две важнейшие теоремы:
-теорема Гаусса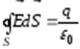 
,
-теорема о циркуляции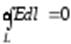 
.
Найдем аналогичные соотношения для 
.
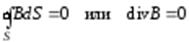. (3.23)
Это теорема Гаусса для вектора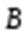 
. Из соотношения(3.23) следует, что магнитные заряды отсутствуют. Линии 
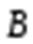не имеют начала и конца, они либо замкнуты, либо уходят на бесконечность.
Теперь рассмотрим теорему о циркуляции для
В общем случае, теорема о циркуляции вектора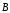 
, или закон полного тока, записывается:
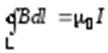, (3.26)
где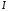 
- полный ток (или сумма токов), охватываемый контуром 
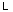. Выведем его в дифференциальной форме. Учтем, что:
;
;
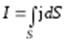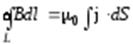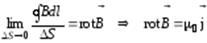, (3.27)
Это - дифференциальная форма закона полного тока. В такой форме он имеет локальный характер и справедлив в любой точке.
Из закона о циркуляции следует, что магнитное поле не потенциально. Так как силовые линии поля замкнуты, то оно является вихревым.
Следующие четыре уравнения для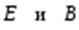 
совместно носят название уравнений Максвелла для вакуума:
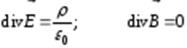; (3.29)
. (3.30)
Физический смысл этих уравнений таков.
· Уравнения (3.29) описывают тот факт, что силовые линии электрического поля начинаются на положительных зарядах и заканчиваются на отрицательных; силовые линии магнитного поля замкнуты (поле вихревое).
· Уравнения (3.30) показывают, что электростатическое поле потенциально; магнитное поле, создаваемое токами (движущимися зарядами), не потенциальное, вихревое.
