Движение заряженных частиц в проводниках под действием приложенного электрического поля назвали электрическим током.
Подвижными заряженными частицами в металлах являются электроны. Носители тока в полупроводниках - также электроны; в электролитах – ионы, в плазме – ионы и электроны.
Основной характеристикой тока является плотность тока  :
:
 , (5.1)
, (5.1)
где  - средняя скорость электрона. Видно, что вектор
- средняя скорость электрона. Видно, что вектор  направлен вдоль скорости движения положительных зарядов.
направлен вдоль скорости движения положительных зарядов.
Через площадку  за единицу времени протекает количество электронов (количество электричества):
за единицу времени протекает количество электронов (количество электричества):
 . (5.2)
. (5.2)
Тогда  - сила тока, проходящего через площадку
- сила тока, проходящего через площадку  . Единицей измерения плотности тока
. Единицей измерения плотности тока  является
является  , силы тока
, силы тока  - А (ампер).
- А (ампер).
Рассмотрим произвольную замкнутую поверхность  (рис.5.1) и найдем поток вектора
(рис.5.1) и найдем поток вектора  сквозь эту поверхность:
сквозь эту поверхность:

 , (5.3)
, (5.3)
где 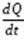 - изменение заряда в единицу времени.
- изменение заряда в единицу времени.
 .
.
Знак “-” показывает, что если число положительных зарядов в объеме уменьшается, то поток  направлен из объема
направлен из объема  наружу.
наружу.
 ;
;
 . (5.4)
. (5.4)
Уравнение (5.4) представляет собой уравнение непрерывности, выражающее закон сохранения заряда в объеме.
Сравним его с теоремой Гаусса в дифференциальной форме:
 ;
;
Смысл уравнения в том, что источниками  являются заряды
являются заряды  . Значит, из уравнения непрерывности следует, что источником тока является временное изменение заряда, токовые силовые линии начинаются там, где
. Значит, из уравнения непрерывности следует, что источником тока является временное изменение заряда, токовые силовые линии начинаются там, где  .
.
Для постоянного тока 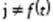 ,
,  , то есть
, то есть  ,
,  : токовые линии всегда замкнуты для постоянного тока.
: токовые линии всегда замкнуты для постоянного тока.
Выясним условия, при которых может существовать постоянный ток. Для этого нужны сторонние источники, создающие направленное движение зарядов ( ). Связь
). Связь  с
с  (напряженность стороннего поля) предполагается линейной:
(напряженность стороннего поля) предполагается линейной:
 - (5.5)
- (5.5)
Здесь  - коэффициент электропроводности;
- коэффициент электропроводности;  . Эта формула верна в точке проводника, где
. Эта формула верна в точке проводника, где  и
и  постоянны, то есть имеет локальный характер, и носит название закона Ома в дифференциальной форме. Открыт Омом в 1827 г. Кавендиш установил экспериментально пропорциональность тока и напряжения еще в 1770 г., но никому об этом не сообщил.
постоянны, то есть имеет локальный характер, и носит название закона Ома в дифференциальной форме. Открыт Омом в 1827 г. Кавендиш установил экспериментально пропорциональность тока и напряжения еще в 1770 г., но никому об этом не сообщил.
Ясно, что установление постоянного значения  после включения
после включения  происходит очень быстро.
происходит очень быстро.
Куда уходит энергия, получаемая электронами в процессе разгона? На преодоление сил ”трения”, то есть на столкновения электронов с решеткой, что приводит к ее нагреванию. При движении заряда совершается работа  . В единице объема выделится энергия:
. В единице объема выделится энергия:
 (5.9)
(5.9)
Значит, за единицу времени в единице объема выделится энергия:
 . (5.10)
. (5.10)
Данная величина носит название тепловой мощности. Иначе:
 . (5.11)
. (5.11)
Закон Джоуля (1841г.), Ленца (1842 г.) в дифференциальной форме, записанный выше, верен в локальной точке проводника.
Интегральный вид этого закона можно вывести, зная количество тепла, выделившегося в проводнике объема  за время
за время  . Введем величину удельного сопротивления:
. Введем величину удельного сопротивления:
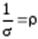 . (5.12)
. (5.12)
Тогда, используя (5.9), запишем:
 . (5.13)
. (5.13)
Для линейного проводника  , где
, где  - площадь сечения,
- площадь сечения,  - элемент длины,
- элемент длины,  . С учетом этого выражение (5.13) примет следующий вид:
. С учетом этого выражение (5.13) примет следующий вид:
 ;
;
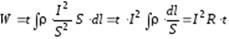 ;
;
 , (5.14)
, (5.14)
где величина  характеризует сопротивление проводника. Подставляя выражение (5.14) в (5.11), получаем окончательно выражение для тепловой мощности:
характеризует сопротивление проводника. Подставляя выражение (5.14) в (5.11), получаем окончательно выражение для тепловой мощности:
 . (5.11 ’)
. (5.11 ’)
Единицей измерения мощности является ватт  .
.
 2020-06-08
2020-06-08 107
107








