Уточнение интересующего решения до требуемой точности ε производится итерационными методами.
Основные методы уточнения решений СНУ получены путем обобщения итерационных процессов, используемых при решении одного нелинейного уравнения.
5.1.3. Метод Ньютона.
Идея метода заключается в линеаризации уравнений системы (5.1), что позволяет свести исходную задачу решения СНУ к многократному решению системы линейных уравнений.
Рассмотрим, как были получены расчетные зависимости метода.
Пусть известно приближение xi(k) решения системы нелинейных уравнений xi*. Введем в рассмотрение поправку Dxi как разницу между решением и его приближением:
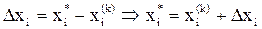 ,
, 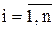
Подставим полученное выражение для xi* в исходную систему.
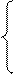
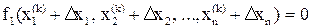
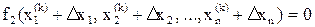
…
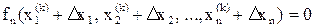
Неизвестными в этой системе нелинейных уравнений являются поправки Dxi. Для определения Dxi нужно решить эту систему. Но решить эту задачу так же сложно, как и исходную. Однако эту систему можно линеаризовать, и, решив ее, получить приближенные значения поправок Dxi для данного приближения, т.е. Dxi(k). Эти поправки не позволяют сразу получить точное решение 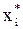 , но дают возможность приблизиться к решению, – получить новое приближение решения
, но дают возможность приблизиться к решению, – получить новое приближение решения
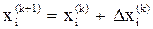 ,
, 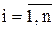 (5.1.4)
(5.1.4)
Для линеаризации системы следует разложить функцию fi в ряды Тейлора в окрестности xi(k), ограничиваясь первыми дифференциалами.
Полученная система имеет вид:
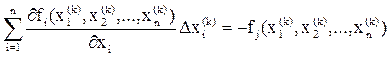 ,
, 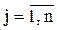 (5.1.5)
(5.1.5)
Все коэффициенты этого уравнения можно вычислить, используя последнее приближение решения xi(k). Для решения системы линейных уравнений (5.1.5) при n=2,3 можно использовать формулы Крамера, при большей размерности системы n – метод исключения Гаусса.
Значения поправок используются для оценки достигнутой точности решения. Если максимальная по абсолютной величине поправка меньше заданной точности e, расчет завершается. Таким образом, условие окончания расчета:
δ = 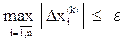
Можно использовать и среднее значение модулей поправок:
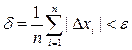 или норму
или норму 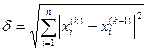
В матричной форме систему (5.1.5) можно записать как:
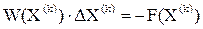 (5.16)
(5.16)
где:
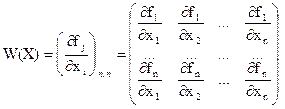 , - матрица Якоби (производных),
, - матрица Якоби (производных),
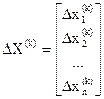 - вектор поправок
- вектор поправок
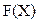 - вектор-функция
- вектор-функция
W(X(k)) – матрица Якоби, вычисленная для очередного приближения.
F(X(k)) – вектор-функция, вычисленная для очередного приближения.
Выразим вектор поправок ∆X(k) из (5.1.6):
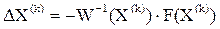
где W-1 – матрица, обратная матрице Якоби.
Окончательно формула последовательных приближений метода Ньютона решения СНУ в матричной форме имеет вид:
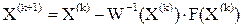 (5.1.7)
(5.1.7)
Достаточные условия сходимости для общего случая имеют очень сложный вид, и на практике проверяются редко. Нужно отметить, что метод сходится очень быстро (за 3 – 5 итераций), если det|W| ¹ 0 и начальное приближение X(0) выбрано близким к решению (отличаются не более чем на 10%).
Алгоритм решения СНУ методом Ньютона состоит в следующем:
1. Задается размерность системы n, требуемая точность ε, начальное приближенное решение X = (xi)n.
2. Вычисляются элементы матрицы Якоби W = (¶¦i ¤ ¶xj)n,n.
3. Вычисляется обратная матрица W-1.
4. Вычисляется вектор функция F=(fi)n, 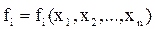 ,
, 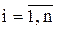 .
.
5. Вычисляются вектор поправок 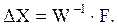
6. Уточняется решение 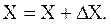
7. Оценивается достигнутая точность δ= 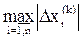 или
или 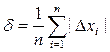 или
или 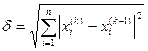
8. Проверяется условие завершения итерационного процесса
δ≤ε
Если оно не соблюдается, алгоритм исполняется снова с пункта 2.
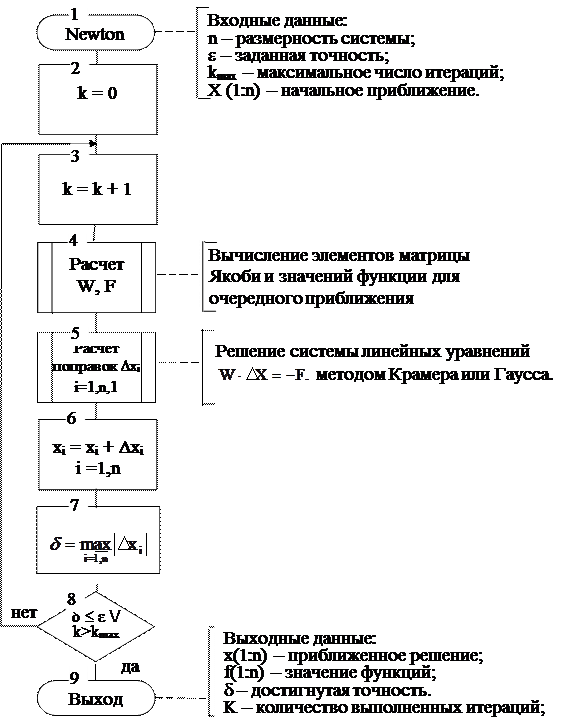 |
Рис 5.3. Схема алгоритма решения СНУ методом Ньютона – Рафсона.
Для уменьшения количества арифметических действий Рафсон предложил не вычислять обратную матрицу W-1, а вычислять поправки как решение СЛУ (5.1.5)
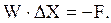
Схема алгоритма метода Ньютона - Рафсона представлена на рис.5.3. При разработке схемы учтена необходимость защиты итерационного цикла от зацикливания: введен счетчик итераций k и ограничение на число итераций kmax (на практике не более 100).
Достоинством методов Ньютона является быстрая сходимость, недостатками - сложность расчетов (вычисление производных, многократное решение системы линейных уравнений), сильная зависимость от начального приближения.
5.1.4. Метод простой итерации
Как и в случае одного уравнения, метод простых итераций заключается в замене исходной системы уравнений ( 5.1 ) эквивалентной системой
X=Φ(X) (5.3)
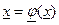 , т. е.
, т. е. 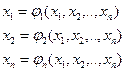 ,
,
где функции 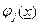 - действительны, определены и непрерывны в некоторой окрестности
- действительны, определены и непрерывны в некоторой окрестности 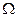 (
(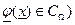 ) изолированного решения
) изолированного решения 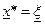 этого уравнения, то итерационная формула имеет вид:
этого уравнения, то итерационная формула имеет вид:
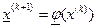 , где k=0,1,2,… (5.3.1)
, где k=0,1,2,… (5.3.1)
Здесь 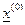 - начальное приближение к корню
- начальное приближение к корню 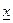 *.
*.
Замечание 1. Если процесс итераций (5.3.1) сходится, т.е. 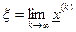 , то он сходится к решению:
, то он сходится к решению: 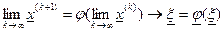 и
и 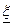 есть корень исходного уравнения (5.3).
есть корень исходного уравнения (5.3).
Замечание 2. Если приближение 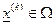 и
и 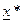 - единственный корень системы (5.3) в
- единственный корень системы (5.3) в 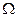 , то
, то 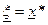 .
.
Достаточное условие сходимости. Процесс итераций ((5.3.1) сходится, если
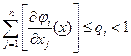 , (5.3.2)
, (5.3.2)
где (i=1,2,…,n) при 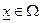 , где
, где 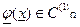 .
.
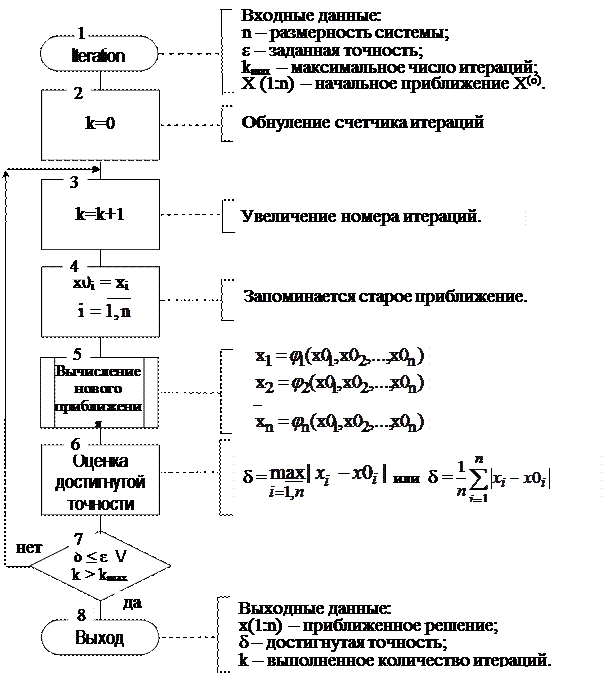
Построение итерационной последовательности
X(k+1) = Φ(X(k)), где k=1,2,3,… - номер итерации, (5.4)
которая при k→∞ сходится к точному решению.
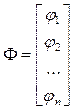 Здесь - итерирующая вектор-функция, X(0)
Здесь - итерирующая вектор-функция, X(0) 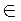 D – начальное
D – начальное
приближение решения.
В развернутом виде формула итерационного процесса (выражение для вычисления очередного k-го приближения решения) имеет вид:
xi.(k+1) = φi(x1(k), x2(k), …, xn(k)), 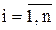 . (5.5)
. (5.5)
Условие окончания расчета
δ≤ε (5.6)
где ε - заданная точность решения;
δ = 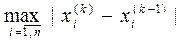 (5.7)
(5.7)
или
δ = 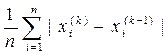 или
или 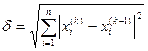 (5.8)
(5.8)
Итерационный процесс (5.5) сходиться к точному решению, если в окрестности решения соблюдаются условия сходимости:
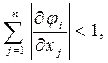
 (5.9)
(5.9)
или
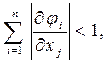
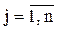 (5.10)
(5.10)
Таким образом, для уточнения решения СНУ методом простых итераций нужно найти такое эквивалентное преобразование (5.1) в (5.3), чтобы в области существования решения выполнялись условия (5.9) или (5.10).
В простейшем случае эквивалентную систему можно получать как:
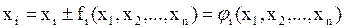 ,
, 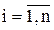
Можно выделить (не обязательно явно) все неизвестные из уравнений системы так, что:
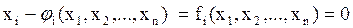 ,
, 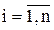
Как и в случае одного уравнения задачу поиска эквивалентного преобразования можно свести к задаче определения (в простейшем случае подбора) значений констант li ≠ 0, 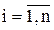 , обеспечивающих сходимость
, обеспечивающих сходимость
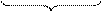
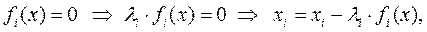
 |
или 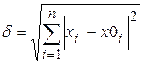
Рис. 5.4. Схема алгоритма метода простых итераций.
Метод Зейделя
Сходимость метода простых итераций можно несколько улучшить, если при вычислении очередного приближения 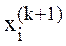 использовать уже найденные значения
использовать уже найденные значения 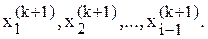
Выражение для расчета очередного к-го приближения примет вид:
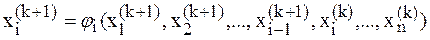 ,
, 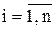 ; (5.11)
; (5.11)
Или после преобразования системы (5.1) к приведенному виду:
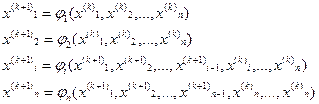
Для реализации данного приема, аналогичного методу Зейделя для систем линейных уравнений, в алгоритм расчета следует внести изменения: формулу расчета очередного приближения (блок 5) записать как X=φ(x) или в развернутом виде:
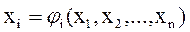 ,
, 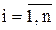
Существуют и другие приемы улучшения сходимости метода простых итераций. Например, новое приближение вычислять как среднее арифметическое двух предшествующих приближений:
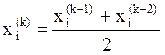 ,
, 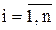 (5.12)
(5.12)
Можно использовать поправку Эйткена для улучшения сходимости:
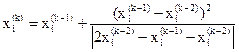 ,
, 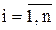
Условия выхода из итерационного цикла можно представить в различных формах, т.е.
 2020-06-08
2020-06-08 647
647







