
Подставляя найденные значения для D1р и d11 в уравнение (8.6) и решая его относительно Х1, найдем:

Суммарные изгибающие моменты в “характерных” сечениях балки найдем из выражения:
 (8.8)
(8.8)
где n - число “лишних” неизвестных или степень статической неопределимости системы; i - номер “характерного” сечения.
Для рассматриваемой балки:



Откладываем найденные значения от базисной линии и строим эпюру суммарных изгибающих моментов (рис. 8.15, з).
Для построения эпюры поперечных сил вырежем часть балки, расположенную между сечениями №1 и №3, приложим все действующие на вырезанный участок силы (рис. 8.16) и составим два уравнения равновесия, из которых найдем значения поперечной силы в “характерных” сечениях, расположенных на границах вырезанного участка:



Рис. 8.16
Учитывая, что  (знак момента учтен выбором его направления), из первого уравнения находим:
(знак момента учтен выбором его направления), из первого уравнения находим:  . Из второго уравнения находим
. Из второго уравнения находим  . По найденным значениям строим суммарную эпюру поперечной силы (рис. 8.15, и).
. По найденным значениям строим суммарную эпюру поперечной силы (рис. 8.15, и).
Особенно обстоятельно они разработаны для рам с прямолинейными стержнями постоянного сечения. Жесткость EI = const при этом выносится за знак интеграла, а под интегралом остается произведение двух функций: Mi и Mk, одна из которых, как правило, или обе являются линейными функциями. Операция интегрирования здесь часто называется перемножением эпюр и ее символически изображают следующим образом:
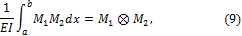
здесь знак  означает умножение в смысле формулы Мора.
означает умножение в смысле формулы Мора.
Применение готовых формул показано в таблице 1. Сами эти формулы без труда определяются элементарными методами. Эта таблица является весьма универсальной, так как она пригодна для определения перемещений по двум любым прямолинейным эпюрам, а также криволинейной с прямолинейной. Если любая из фигур, приведенных в табл. 1, перемножается с треугольником, то это перемножение сводится к трапеции, одна из ординат которых равна 0. При перемножении на прямоугольник нужно учесть, что Мa = Мb.
При помощи расчленения эпюр на части можно добиться того, чтобы при перемножении участвовали эпюры простой структуры, приведенные в таблице 1.
Таблица 1
| M 2(x) M 1(x) | 
| 
| 
| 
| 
| 
| 
|

| abl | 
| 
| 
| 
| 
| 
|

| 
| 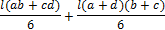
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
| 
| 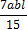
|

| 
| 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 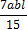
| 
| 
|
Например, пусть нужно перемножить эпюры, приведенные на рис. 32. Каждую из эпюр можно представить в виде суммы: в первом случае, в виде двух треугольных и параболической; во втором -в виде двух треугольных.

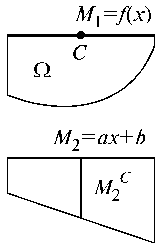
Рис. 32 Рис. 33
Итак,

Тогда



А далее следует воспользоваться формулой для вычисления интегралов  , приведенных в таблице 1.
, приведенных в таблице 1.
Довольно удобным способом перемножения эпюр является способ Верещагина. Этот способ применим в случае когда из двух перемножаемых эпюр одна как минимум является прямолинейной. Если одна из эпюр является криволинейной вычисляется площадь  криволинейной эпюры, которая умножается на ординату под ее центром тяжести, взятую в прямолинейной эпюре
криволинейной эпюры, которая умножается на ординату под ее центром тяжести, взятую в прямолинейной эпюре  (рис.33).
(рис.33).
Предположим M 1 = f (x); M 2 = a x + b, тогда

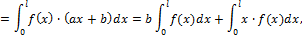
но величина  представляет собой площадь криволинейной эпюры, а величина
представляет собой площадь криволинейной эпюры, а величина  - статический момент площади этой эпюры относительно левого конца стержня. Следовательно,
- статический момент площади этой эпюры относительно левого конца стержня. Следовательно,
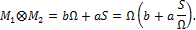
Известно, что величина  представляет собой ординату центра тяжести криволинейной эпюры, а
представляет собой ординату центра тяжести криволинейной эпюры, а  - значение M 2 при
- значение M 2 при  .
.
В случае двух криволинейных эпюр способ Верещагина неприменим. Надо пользоваться интегралом Мора. Способ Верещагина применим также в тех случаях, когда одна из эпюр не криволинейная, а ломаная.
В таблице 2 приведены формулы для определения площади  , положения центра тяжести zC и ординаты yC в центре тяжести для некоторых довольно распространенных плоских фигур.
, положения центра тяжести zC и ординаты yC в центре тяжести для некоторых довольно распространенных плоских фигур.
В случае, когда имеются эпюры общего вида (например, обе эпюры криволинейные, либо трапеции, рис.33, разбиение уже на два равных интервала дает согласно формуле Симпсона точное выражение интеграла:

где индексы А и С относятся к сечениям расположенным на концевых сечениях интервала длиной l, а индекс В к серединному сечению того же интервала.
В тех случаях, когда функции M 1 и M 2 в рассматриваемом интервале длиной l, являются линейными и известны их значения в концевых сечениях интервала, то формулу перемножения M 1 и M 2 можно преобразовать в следующем виде:

Итак, после составления и решения канонической системы уравнений метода сил (7.4) мы получаем значения X 1, X 2, X 3,..., Xn, т.е. значения усилий в лишних связях. Затем строим для основной системы эпюры изгибающих моментов от каждого из найденных усилий. Для этого могут быть использованы построенные ранее единичные эпюры, все ординаты которых необходимо теперь умножить на найденные значения соответствующих неизвестных.
Сложив по характерным сечениям (на протяжении всей рассчитываемой конструкции) ординаты эпюр от действия всех сил Xi с ординатами грузовой эпюры, получим окончательную (суммарную) эпюру изгибающих моментов в заданной статически неопределимой системе.
Таблица 2
| № | Фигура | Площадь | Абсциссы центра тяжести | |
| z 1 | z 2 | |||
| 1 | 
| yl | 
| 
|
| 2 | 
|

|

|

|
| 3 | 
|

|

|

|
| 4 | 
|

|

|

|
| 5 | 
|

|

|

|


Пример 1.
Требуется раскрыть статическую неопределимость балки и построить эпюры изгибающих моментов и поперечных сил (рис.34, а).
Решение.
В сечении А балка имеет жесткую опору, исключающую перемещение и поворот сечения. Такая опора соответствует наличию трех связей. На правом конце балка опирается свободно и имеет одну связь. Таким образом, балка имеет четыре связи при трех степенях свободы. Степень статической неопределимости балки равна единице.
Изобразим балку и расставим “характерные” сечения: на левом конце, посредине и на правом конце (рис.34, а). Оборвем одну связь в сечении В и действие связи заменим реакцией  (рис.34, б). Величина этой реакции неизвестна, но она должна быть такой, чтобы вертикальное перемещение сечения В было равно нулю. В этом условии будет заключаться эквивалентность исходной системы (рис.34, а) и статически определимой системе, изображенной на рис.34, б. Чтобы описать условие эквивалентности двух систем, воспользуемся принципом независимости сил, сначала изобразим балку, нагрузив ее только внешней нагрузкой (рис.34, в). Перемещение сечения В, вызванное внешней нагрузкой, обозначим
(рис.34, б). Величина этой реакции неизвестна, но она должна быть такой, чтобы вертикальное перемещение сечения В было равно нулю. В этом условии будет заключаться эквивалентность исходной системы (рис.34, а) и статически определимой системе, изображенной на рис.34, б. Чтобы описать условие эквивалентности двух систем, воспользуемся принципом независимости сил, сначала изобразим балку, нагрузив ее только внешней нагрузкой (рис.34, в). Перемещение сечения В, вызванное внешней нагрузкой, обозначим  . Далее изобразим балку, нагруженную только сосредоточенной силой
. Далее изобразим балку, нагруженную только сосредоточенной силой 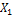 . Перемещение сечения В, вызванное этой нагрузкой, обозначим
. Перемещение сечения В, вызванное этой нагрузкой, обозначим 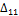 . Сумма этих перемещений должна равняться нулю, так как в исходной системе сечение В в вертикальном направлении не перемещается:
. Сумма этих перемещений должна равняться нулю, так как в исходной системе сечение В в вертикальном направлении не перемещается:

Уравнение (19) удобно записывать в канонической форме:

где  . Здесь
. Здесь  - перемещение, вызванное силой, равной единице, приложенной в сечении В (рис.34, е).
- перемещение, вызванное силой, равной единице, приложенной в сечении В (рис.34, е).
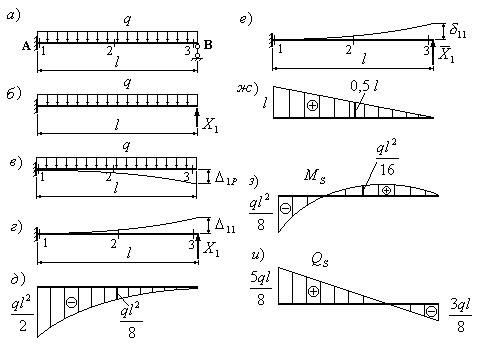
Рис.34
Неизвестную реакцию 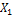 можно определить из уравнения (20), если предварительно найти перемещение
можно определить из уравнения (20), если предварительно найти перемещение  , которое назовем грузовым, и перемещение
, которое назовем грузовым, и перемещение  , которое назовем единичным.
, которое назовем единичным.
Чтобы определить грузовое перемещение  , построим грузовую эпюру изгибающих моментов (рис.34, д), единичную эпюру (рис.34, ж) и перемножим их, воспользовавшись формулой Мора-Симпсона:
, построим грузовую эпюру изгибающих моментов (рис.34, д), единичную эпюру (рис.34, ж) и перемножим их, воспользовавшись формулой Мора-Симпсона:

В рассматриваемом примере:
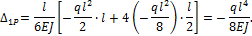
Единичное перемещение  найдем, умножив единичную эпюру (рис.34, ж) саму на себя.
найдем, умножив единичную эпюру (рис.34, ж) саму на себя.
 2020-06-08
2020-06-08 441
441








