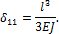
Подставляя найденные значения для  и
и  в уравнение (20) и решая его относительно
в уравнение (20) и решая его относительно 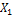 , найдем:
, найдем:

Суммарные изгибающие моменты в “характерных” сечениях балки найдем из выражения:
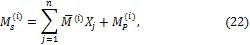
где n - число “лишних” неизвестных или степень статической неопределимости системы; i - номер “характерного” сечения.
Для рассматриваемой балки:

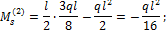
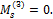
Откладываем найденные значения от базисной линии и строим эпюру суммарных изгибающих моментов (рис.34, з).
Для построения эпюры поперечных сил вырежем часть балки, расположенную между сечениями №1 и №3, приложим все действующие на вырезанный участок силы (рис.35) и составим два уравнения равновесия, из которых найдем значения поперечной силы в “характерных” сечениях, расположенных на границах вырезанного участка:



Рис.35
Учитывая, что 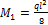 (знак момента учтен выбором его направления), из первого уравнения находим:
(знак момента учтен выбором его направления), из первого уравнения находим: 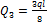 . Из второго уравнения находим
. Из второго уравнения находим 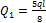 . По найденным значениям строим суммарную эпюру поперечной силы (рис.34, и).
. По найденным значениям строим суммарную эпюру поперечной силы (рис.34, и).
Пример 2.
Для балки (рис. 36, а) определим внутренние усилия.
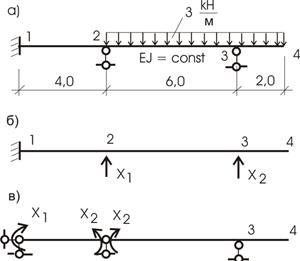
Рис.36
Решение.
1) Рассчитаем степень статической неопределимости n =5-3=2.
Два раза статически неопределимая балка. Основные системы метода сил представлены на рисунке 36, б,в.
Для расчета примем вариант 36, в.
2) Запишем систему канонических уравнений:
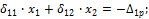

3) Вычисляем коэффициенты 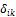 и
и  .
.
Эпюры от единичных загружений представлены на рисунке 37, б,в и от внешней нагрузки - на рисунке 37, г.
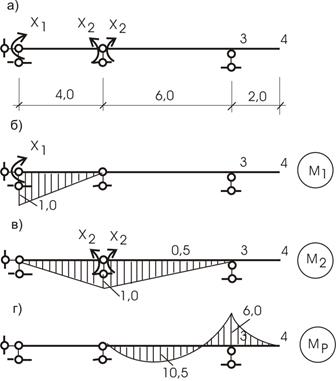
Рис.37

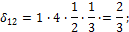
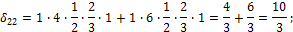
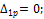
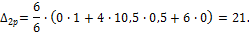
Решение системы:
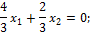
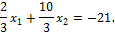
дает 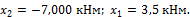
По полученным значениям строим 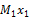 и
и 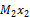 (рис. 38, а,б)
(рис. 38, а,б)
и 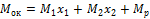 (рис. 38, в).
(рис. 38, в).
Проверки.
а) Статическая проверка. Значения моментов на опорах (рис. 38, в) одинаковы и равновесие обеспечивается. Проверка удовлетворяется.
б) Кинематическая проверка.
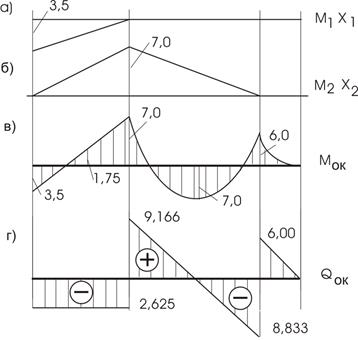
Рис.38
Перемножим 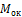 с
с 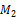 . Проверим, будет ли взаимный угол поворота сечений балки на опоре 2 равен нулю?
. Проверим, будет ли взаимный угол поворота сечений балки на опоре 2 равен нулю?
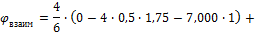
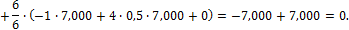
Проверка удовлетворяется.
Эпюра 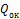 строится по эпюре
строится по эпюре 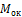 по рассмотренному ранее принципу. Выполните построение самостоятельно и свой результат сверьте с приведенным решением на рис.38, г.
по рассмотренному ранее принципу. Выполните построение самостоятельно и свой результат сверьте с приведенным решением на рис.38, г.
Пример 3.
Определить усилия (в кН) в стержнях фермы, изображенной на рис.39.

Рис.39
Решение.
1. Определяем степень статической неопределимости: n=3-2=1.
2. Выбираем основную систему (рис.40).Основная система получается из заданной путем рассечения одного из стержней, например, стержня ВС.
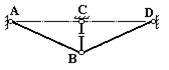
Рис.40. Основная система
3. Изображаем эквивалентную систему (рис.41).
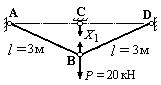
Рис.41. Эквивалентная система
Каноническое уравнение метода сил имеет вид:
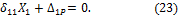
Физический смысл этого уравнения состоит в том, что взаимное перемещение сечений, которые получились при рассечении стержня ВС, равно нулю.
4. Изображаем грузовое состояние системы (рис.42) и определяем усилия в стержнях фермы АВ и ВD.
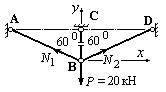
Рис.42. Грузовое состояние системы
Составляем уравнения равновесия сил на оси x и y:
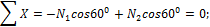
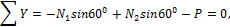
откуда находим:

5. Изображаем единичное состояние системы (рис.43) и находим единичные усилия в стержнях фермы:
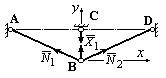
Рис.43. Единичное состояние системы
Составляем уравнения равновесия на оси x и y:
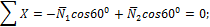

откуда находим:
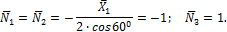
6. Определяем грузовое  и единичное перемещения
и единичное перемещения  . Для этого воспользуемся формулой Максвелла:
. Для этого воспользуемся формулой Максвелла:
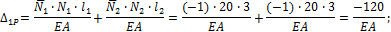
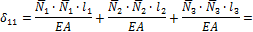

Из канонического уравнения (23) находим “лишнюю” неизвестную 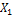 :
:
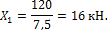
Усилия в стержнях 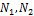 и
и 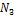 найдем из формулы:
найдем из формулы:
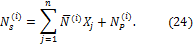
Подставляя в формулу (24) значения “лишней” неизвестной, грузовых и единичных изгибающих моментов, получаем:
Пример 4.
Определить реакцию опоры В рамы, изображенной на рис.44.
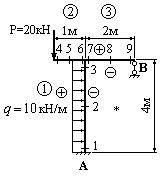
Рис.44
Следует отметить, что в заданной постановке можно избежать построения суммарных эпюр изгибающих моментов и поперечных сил для определения реакции опоры В. Для этого нужно выбрать таким образом основную систему, чтобы связь в опоре В оказалась “лишней”. Тогда “лишняя” неизвестная, заменяющая действие “лишней” связи, и будет искомой реакцией.
Решение.
1. Разбиваем раму на участки, выбираем точку наблюдения, вводим положительные и отрицательные стороны и проставляем “характерные” сечения.
2. Определяем степень статической неопределимости: n=4-3=1.
3. Выбираем основную систему. Так как нас интересует реакция опоры В, принимаем в качестве “лишней” неизвестной 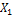 реакцию в этой опоре (рис.45).
реакцию в этой опоре (рис.45).
Рис.45. Основная система
4. Изображаем эквивалентную систему (рис.46).
Рис.46. Эквивалентная система
Каноническое уравнение метода сил имеет вид:

Физический смысл этого уравнения – равенство нулю перемещений в направлении “лишней” неизвестной 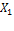 , вызванное самой “лишней” неизвестной и внешней нагрузкой.
, вызванное самой “лишней” неизвестной и внешней нагрузкой.
5. Изображаем грузовое состояние системы (рис.47, а) и строим грузовую эпюру изгибающих моментов 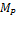 (рис.47, б).
(рис.47, б).
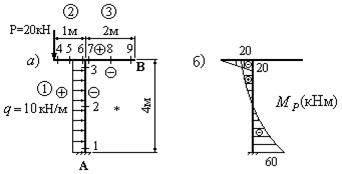
Рис.47
6. Изображаем единичное состояние системы (рис.48, а) и строим единичную эпюру изгибающих моментов 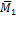 (рис.48, б).
(рис.48, б).
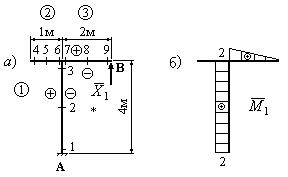
Рис.48
7. Перемножая грузовую эпюру 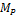 и единичную эпюру
и единичную эпюру 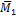 изгибающих моментов по формуле Мора-Симпсона, находим грузовое перемещение
изгибающих моментов по формуле Мора-Симпсона, находим грузовое перемещение  :
:
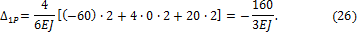
8. Перемножая единичную 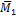 изгибающих моментов саму на себя, находим единичное перемещение
изгибающих моментов саму на себя, находим единичное перемещение  :
:
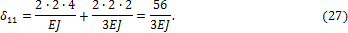
Подставляя (26) и (27) в уравнение (25) и решая его относительно 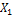 , получим:
, получим:

Полученная значение для “лишней” неизвестной 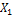 и есть величина опорной реакции В. Положительный знак у реакции означает, что направление “лишней” неизвестной
и есть величина опорной реакции В. Положительный знак у реакции означает, что направление “лишней” неизвестной 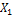 , а, следовательно, и реакции опоры В выбрано верно.
, а, следовательно, и реакции опоры В выбрано верно.
Пример 5.
Для заданной рамы (рис.49) требуется построить эпюры M, Q, N.
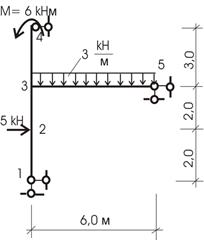
Рис.49
Решение.
1. Определяем степень статической неопределимости n =5-3=2
Для получения основной системы нужно отбросить 2 избыточные связи.
2. Выбираем основную систему.
Варианты основной системы приведены на рисунке 50, а,б,в,г.
Для расчета возьмем вариант 2 (выбор произвольный).
3. Запишем канонические уравнения для решения:
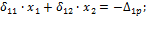
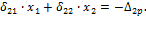
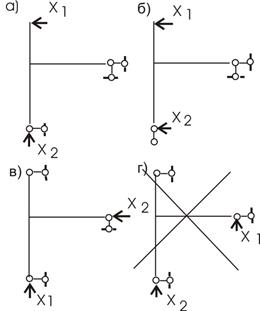
Рис.50
Для подсчета коэффициентов и свободных членов уравнений построим эпюры от единичных сил и внешней нагрузки (рис. 51, а,б,в,г).
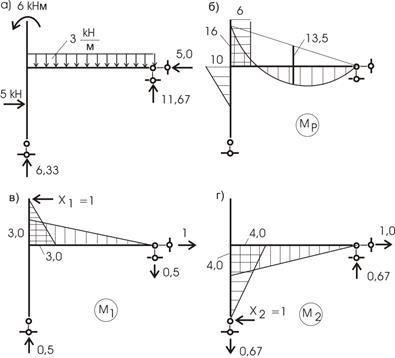
Рис.51
Вычисление основных параметров для построения эп. М от внешней нагрузки:
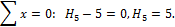
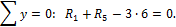
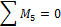
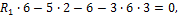

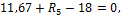
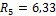
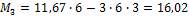
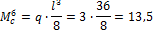
То же для построения М1.
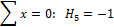
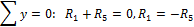
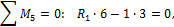

И для построения М2.
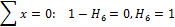
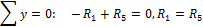
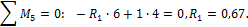
4. Вычисляем коэффициенты при x i по правилу Верещагина:
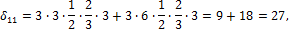
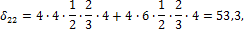
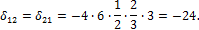
Вычисляем грузовые слагаемые:
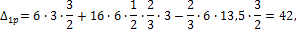
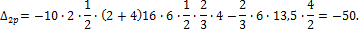
Перед решением системы уравнений производим проверку правильности вычислений коэффициентов:
а) построчная проверка

где 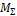 - суммарная эпюра моментов от единичных сил (рис. 52) и для первой строки
- суммарная эпюра моментов от единичных сил (рис. 52) и для первой строки

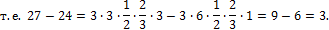
Равенство удовлетворяется.

Рис.52
б) суммарная проверка.
Сумма всех коэффициентов = 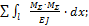
т.е.
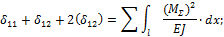
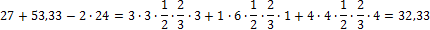
т.е.
32,33=32,33.
Условие удовлетворяется.
в) проверка грузовых слагаемых
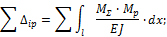
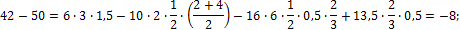
-8=-8.
Условие удовлетворяется.
5. Решение системы производим по методу Гаусса
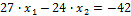
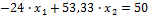
Для этого разделим первое уравнение на 27, а второе – на 24. Получим:
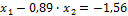
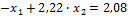
Складываем оба уравнения:
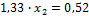
Отсюда находим:
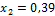
Подставляем х 2 в любое уравнение системы:
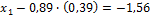
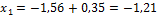
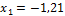
Вывод: Неизвестная реакция х 1 = - 1,21 направлена нами неправильно. Истинное направление реакции Н 4 будет вправо, а направление реакции Н 1 нами выбрано верно.
Дальнейший расчет может производиться двумя путями:
1) Приложив найденные усилия xi к основной системе совместно с внешней нагрузкой (рис. 53), строим обычным способом эпюры Мок, Qок, Nок. Опорные реакции H5, R5, R1 определяются из уравнений статики, и дальнейших пояснений не требуется.
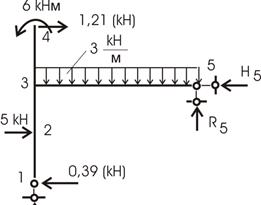
Рис.53
Построение этим путем мы предоставляем читателю для самостоятельного решения.
2) Используем принцип независимости действия сил, а именно:
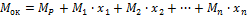
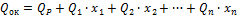
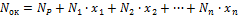
Поскольку эпюры перерезывающих и продольных сил обычно не строятся ни от единичных сил, ни от внешней нагрузки, то эпюра перерезывающих сил Qок строится по эпюре изгибающих моментов Мок, а эпюра Nок - по эпюре Qок.
Рассмотрим этот путь расчета. Для этого построим эпюры Mixi (рис. 54, а,б) и рядом - Мр. (рис. 54, в). Результат построения - эпюра Мок (рис. 54, г).
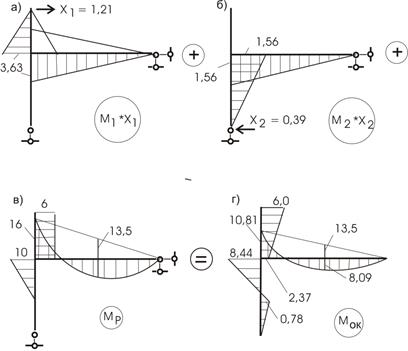
Рис.54
Проверим правильность построения эпюры Мок.
1. Статическая проверка.
Вырезаем узел 3 (рис. 55).
Составим уравнение статики
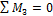 : 2,37+8,44-10,81=0
: 2,37+8,44-10,81=0
Условие удовлетворяется.
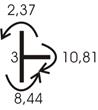
Рис.55
2. Кинематическая проверка.
Проверяем перемещение точки приложения силы xi по ее направлению. Оно должно быть равно нулю, что отвечает условию совместности деформации
Перемножим Мок на М1
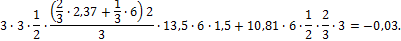
Ошибка составляет
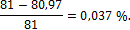
Условие удовлетворяется.
По эпюре Мок строим эпюру Qок. Для этого рассмотрим каждый стержень рамы, как отдельную балку, нагруженную системой сил: изгибающими моментами и внешней нагрузкой (рис.56).

Рис.56
Построив обычным путем эпюры Q для каждого участка, сформируем эпюру Qок (рис.57, а). Эпюра Nок строится по эпюре Qок из условия равновесия узлов:
Вырезаем узел 4 (рис.58, а)
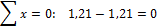
Вырезаем узел 3 (рис.58, б)
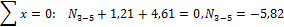

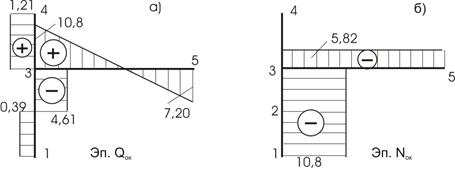
Рис.57

Рис.58
Эпюра Nок показана на рисунке 57, б.
 2020-06-08
2020-06-08 251
251







