Регрессионный анализ. Уравнение регрессии

 

Корреляционная связь предполагает зависимость результативного признака от значений факторного признака. Корреляционный анализ устанавливает наличие и тесноту такой связи, но ничего не говорит о её форме и характере изменений. Это является задачей регрессионного анализа. Он представляет собой метод установления функциональной зависимости между условным средним значением результативного (зависимого) признака от факторных (независимых) признаков. При этом предполагается, что результативный признак подчиняется нормальному закону распределения, а факторный признак может иметь произвольный характер распределения. 

Термин «регрессия» был впервые использован Фрэнсисом Гальтоном ещё в 1877 году.

Графически регрессия представляет собой теоретическую линию, вокруг которой группируются точки корреляционного поля и которая указывает основное направление, основную тенденцию корреляционной связи. Теоретическая линия регрессии отображает изменение средних величин результативного признака y по мере изменения величин факторного признака x при условии полного взаимопогашения всех случайных причин. В идеале сумма отклонений точек поля корреляции от соответствующих точек линии регрессии должна быть равна нолю, а сумма квадратов этих отклонений быть минимальной величиной.

В статистике выделяют различные виды регрессионных моделей.

Парная регрессия представляет собой регрессию между двумя переменными. В качестве примера можно назвать зависимость прибыли предприятия (зависимая переменная) от производительности труда (объясняющая переменная);

Множественная регрессия – регрессия между зависимой переменной у и несколькими причинно обусловленными объясняющими (независимыми, или предсказывающими) х₁ х₂,..., х_n. Так, имеется множественная регрессия между прибылью предприятия (y) и производительностью труда (x₁), объёмом основных фондов (x₂), объёмом оборотных средств (x₃).

Требования к построению регрессионной модели:

1) совокупность исследуемых данных должна быть однородной и описываться непрерывными функциями;

2) все факторные признаки должны иметь количественное выражение;

3) объём исследуемой статистической совокупности должен быть достаточно большим;

4) должна прослеживаться причинно-следственная связь между изучаемыми явлениями или процессами;

5) территориальная и временная структура статистической совокупности должна быть постоянной.

Этапы регрессионного анализа:

1) построение поля корреляции и выдвижение гипотезы о форме связи;

2) расчёт параметров предполагаемого уравнения регрессии;

3) интерпретация полученных результатов;

4) оценка статистической значимости уравнения регрессии.

Главной задачей регрессионного анализа является определение типа функции, с помощью которой характеризуется зависимость между признаками. Главным основанием для выбора уравнения регрессии должен служить содержательный анализ природы изучаемой зависимости, её механизма. Помогает и графическое изображение корреляционного поля, задающего эмпирическую линию регрессии.

Наиболее часто встречающиеся типы функций для парной регрессии:

Название	Функция
Линейная
Параболическая
Гиперболическая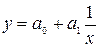
Показательная
Степенная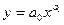
Логарифмическая

Параметры уравнения регресси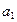и , и 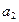находятся при помощи метода наименьших квадратов, разработанного немецким математиком Карлом Фридрихом Гауссом (1777-1855) в 1795 году.

Система нормальных уравнений МНК для линейной парной регрессии имеет следующий вид:

                                                                   

Отсюда можно выразить параметры регрессии:

                                          ;                                    

.

Параметр a₀ – это постоянная величина в уравнении регрессии. Экономического смысла он не имеет, но в ряде случаев его интерпретируют как начальное значение y, т. е. он показывает усреднённое влияние на результативный признак неучтённых факторов. Если a₀>0, то относительное изменение переменной y происходит медленнее, чем изменение переменной x. Если a₀ < 0, то относительное изменение переменной y происходит быстрее, чем изменение переменной x.

Параметр 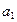в уравнении называется коэффициентом регрессии. Он показывает, насколько в среднем изменяется величина результативного признака y при изменении факторного признака x на единицу. Геометрически коэффициент регрессии представляет собой наклон прямой линии, изображающей уравнение корреляционной зависимости, относительно оси x. Чем больше величина коэффициента регрессии, тем значительнее влияние данного признака на моделируемый.

Положительное значение коэффициента регрессии указывает на наличие прямой связи, отрицательное значение – на обратную связь.

Коэффициент регрессии для линейной парной корреляции можно также определить по формуле:

где r – линейный коэффициент корреляци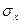и;

и – средние квадратические отклонения значений факторного и результативного признаков.

Коэффициент регрессии применяют для определения коэффициента эластичности, который показывает, на сколько процентов изменится величина результативного признака y при изменении факторного признака x на 1%. Для линейной функции коэффициент эластичности рассчитывается по формуле:

Заключительный этап регрессионного анализа предполагает оценку статистической значимости уравнения регрессии, для чего используется ряд показателей.

1). Средняя квадратическая ошибка уравнения регрессии () представляет собой среднее квадратическое отклонение фактических значений результативного признака от теоретических:

где – фактические значения результативного признака, полученные по данным наблюдения;

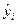 – значения результативного признака, рассчитанные по уравнению регрессии;

  n – количество наблюдений;

m – число параметров в уравнении регрессии.

Для линейной функции средняя квадратическая ошибка принимает вид:

Если полученная средняя квадратическая ошибка уравнения регрессии окажется меньше среднего квадратического отклонения результативного признака (), то использование данного уравнения регрессии является целесообразным.

Средняя квадратическая ошибка уравнения регрессии даёт возможность определить интервал доверительных границ, в которых с определённой вероятностью окажется теоретическое значение результативного признака, вычисленное по уравнению регрессии.

Доверительные границы результативного признака y при значении факторного признака 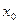определяются следующим образом:

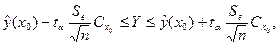
где 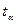определяется в соответствии с уровнем значимости по t -распределению Стьюдента с (n-m) степенями свободы.

Множитель вычисляется для каждого значения 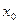и характеризует величину отклонения факторного признака от своего среднего арифметического значения:

Величину средней квадратической ошибки уравнения регрессии можно использовать при выборе вида той или иной функции в качестве уравнения регрессии по критерию:

2). Средняя квадратическая ошибка параметров уравнения регрессии:

а) для коэффициента регрессии :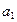      

б) для параметра :

3). Оценка правильности выбора вида взаимосвязи и значимости уравнения регрессии осуществляется через проверку статистической значимости коэффициента детерминации по критерию F -распределения. Расчётное значение F -критерия для линейной функции (m =2) определяется по формуле:

Расчётное значение F -критерия для нелинейной функции зависит от величины эмпирического корреляционного отношения:

Далее расчётное значение сравнивается с табличным при степенях свободы 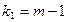и 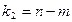. Если 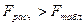, то коэффициент детерминации статистически значим, а выбор уравнения регрессии правилен.

Возможность использования линейной функции в качестве формы уравнения регрессии определяется следующим образом:

1) через разность квадратов эмпирического корреляционного отношения и линейного коэффициента корреляции: если , то считается возможным применить линейное уравнение корреляционной зависимости;

2) через величину , подчиняющуюся закону F -распределения:

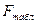Если окажется больше , то гипотезу о линейном виде регрессии можно считать статистически не обоснованной.

В этом случае необходимо использовать нелинейные функции для уравнения регрессии.

 

Пример 2.

По десяти промышленным предприятиям одной отрасли имеются следующие данные за год:

Показатель	Номер предприятия
	1	2	3	4	5	6	7	8	9	10
Основные фонды, млн. руб.	10	13	15	19	22	26	27	30	34	35
Прибыль, млн. руб.	4	5	6	8	9	12	13	15	16	17

По этим данным найти уравнение регрессии, выражающее зависимость прибыли предприятий от величины их основных фондов. Определить коэффициент корреляции прибыли и величины основных фондов.

Решение:

Основные фонды – факторный признак , прибыль – результативный признак .

Уравнение регрессии построим по линейной функции .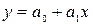

Для вычисления параметров уравнения регрессии произведём ряд предварительных расчётов.

Номер
1	10	4	100	16	40	171,61	42,25
2	13	5	169	25	65	102,01	30,25
3	15	6	225	36	90	65,61	20,25
4	19	8	361	64	152	16,81	6,25
5	22	9	484	81	198	1,21	2,25
6	26	12	676	144	312	8,41	2,25
7	27	13	729	169	351	15,21	6,25
8	30	15	900	225	450	47,61	20,25
9	34	16	1156	256	544	118,81	30,25
10	35	17	1225	289	595	141,61	42,25
Итого	231	105	6025	1305	2797	688,9	202,5

Тогда:

Уравнение регрессии принимает вид: .

Средняя квадратическая ошибка уравнения регрессии:

Среднее квадратическое отклонение факторного признака:

Среднее квадратическое отклонение результативного признака:

Так как 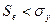, то использование данного уравнения регрессии является целесообразным.

Находим линейный коэффициент корреляции прибыли от величины основных фондов по формуле:

Данное значение коэффициента корреляции говорит об очень тесной прямой корреляционной связи между признаками, близкой к функциональной.

Для оценки статистической значимости корреляционной связи воспользуемся t-критерием Стьюдента:

Табличное значение t-критерия Стьюдента 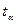 при уровне значимости =0,01 и числе степеней свободы k = n – 2 = 10 – 2 = 8равно 3,355. Так как , то с вероятностью =1–0,01=0,99, или 99%, можно говорить о статистической значимости коэффициента корреляции и наличии корреляционной связи.

Доверительный интервал для линейного коэффициента корреляции: