Методы оценки статистической значимости связи

Для линейного коэффициента корреляции:

1). t- критерий Стьюдента (псевдоним Уильяма Госсета, 1876-1937):

 а) для большого объёма статистической совокупности, распределённой по нормальному закону:

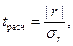
где 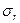 – средняя квадратическая ошибка линейного коэффициента корреляции, определяемая по формуле: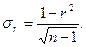

б) для малого объёма статистической совокупности (n < 50):

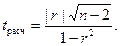
Полученная величина 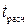 сравнивается с её табличным значением  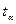при уровне значимости 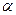=0,05 или 0,01 и числе степеней свободы k = n – 2. Если 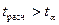, то с вероятностью () можно говорить о статистической значимости коэффициента корреляции. В противном случае наличие корреляционной связи может быть поставлено под сомнение.

Доверительный интервал для линейного коэффициента корреляции: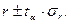

2). Критерий Рональда Фишера (1890-1962) используется для оценки существенности корреляционной связи.

Для этого расчётное значение линейного коэффициента корреляции сравнивается с табличным значением при уровне значимости 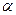(0,05; 0,02; 0,01) и числе степеней свободы k = n – 2. Если расчётное значение превышает табличное, то можно говорить о наличии корреляционной связи между признаками, в противном случае – об отсутствии связи.

3). Метод преобразованной корреляции Рональда Фишера используется для малой статистической совокупности при высоких значениях расчётного коэффициента корреляции ().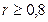

Метод Р. Фишера основан распределении логарифмической функции линейного коэффициента корреляции ( -распределение), которое приближено к нормальному закону распределения:

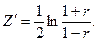
Средняя квадратическая ошибка -распределениязависит только от объёма статистической совокупности:

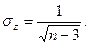
Если отношение 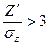 , то наличие корреляционной связи можно считать подтверждённым.