Построение линейной регрессии иллюстрируется на следующем примере:
Пример 1. Задача состоит в построении модели зависимости объясняемой переменной «накопления» (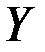 ) от объясняющих переменных «дохода» (
) от объясняющих переменных «дохода» (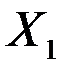 ) и «имущества» (
) и «имущества» (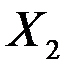 ). Данные приведены на рис.1.
). Данные приведены на рис.1.
В общем случае есть следующие статистические данные 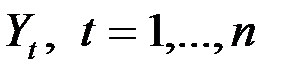 -
- 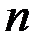 наблюдений объясняемой переменной, а
наблюдений объясняемой переменной, а 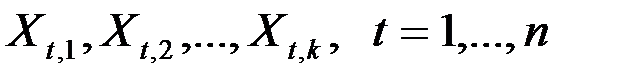 -
- 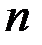 наблюдений
наблюдений 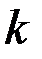 объясняющих переменных. Запишем их в виде таблицы EXCEL, как это сделано на рис.1.
объясняющих переменных. Запишем их в виде таблицы EXCEL, как это сделано на рис.1.
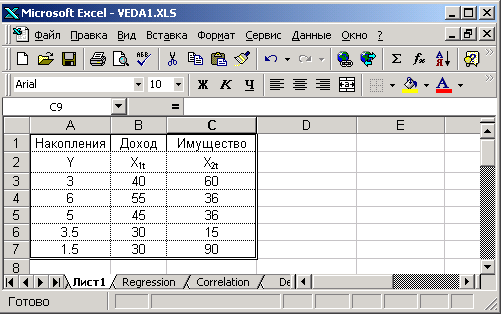
Рис.1
Надо найти оценки коэффициентов модели
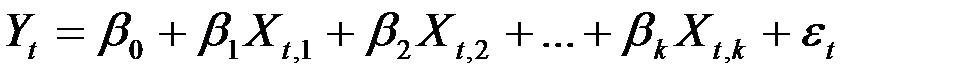 .
.
Для получения отчета по построению модели в среде EXCEL необходимо выполнить следующие действия:
1. 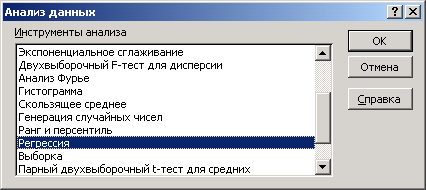
В меню Сервис выбираем строку Анализ данных. На экране появится окно
Рис.2
2. 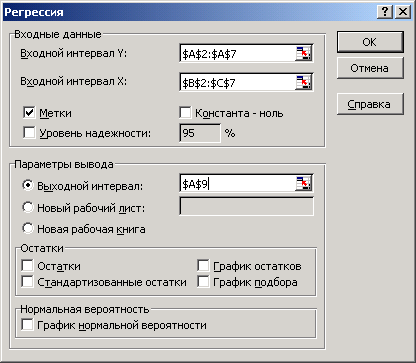
В появившемся окне выбираем пункт Регрессия. Появляется диалоговое окно рис.3.
Рис.3.
3. Диалоговое окно рис.3 заполняется следующим образом:
Входной интервал 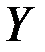 – диапазон (столбец), содержащий данные со значениями объясняемой переменной;
– диапазон (столбец), содержащий данные со значениями объясняемой переменной;
Входной интервал 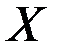 – диапазон (столбцы), содержащий данные со значениями объясняющих переменных.
– диапазон (столбцы), содержащий данные со значениями объясняющих переменных.
Метки – флажок, который указывает, содержат ли первые элементы отмеченных диапазонов названия переменных (столбцов) или нет;
Константа-ноль - флажок, указывающий на наличие или отсутствие свободного члена в уравнении (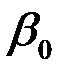 );
);
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона, в котором будет сохранен отчет по построению модели;
Новый рабочий лист – можно задать произвольное имя нового листа, в котором будет сохранен отчет.
Если необходимо получить значения и графики остатков (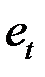 ), установите соответствующие флажки в диалоговом окне. Нажмите на кнопку Ok.
), установите соответствующие флажки в диалоговом окне. Нажмите на кнопку Ok.
Вид отчета о результатах регрессионного анализа представлен на рис.4.
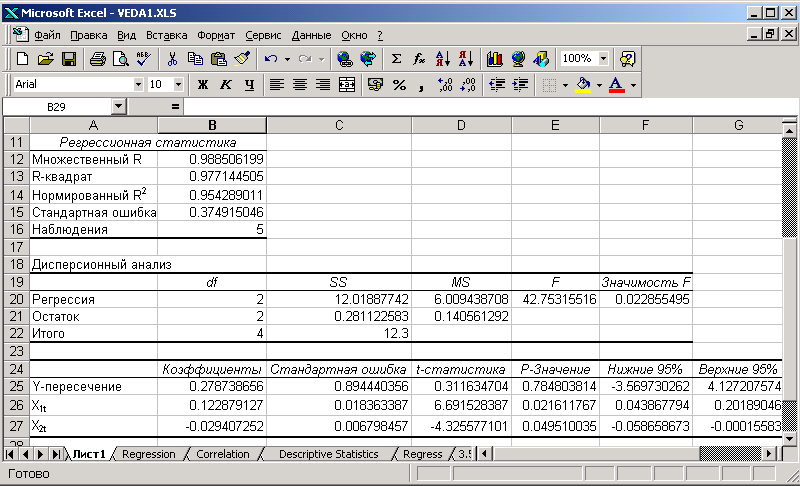
Рис.4.
Множественный R – это 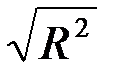 , где
, где 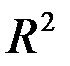 – коэффициент детерминации.
– коэффициент детерминации.
R-квадрат - это 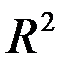 . Коэффициент
. Коэффициент 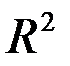 является одной из наиболее эффективных оценок адекватности регрессионной модели, мерой качества уравнения регрессии (или, как говорят, мерой качества подгонки регрессионной модели к наблюденным значениям
является одной из наиболее эффективных оценок адекватности регрессионной модели, мерой качества уравнения регрессии (или, как говорят, мерой качества подгонки регрессионной модели к наблюденным значениям 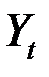 )
)
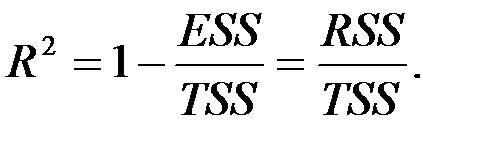
Величина 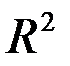 показывает, какая часть (доля) вариации объясняемой переменной обусловлена вариацией объясняющей переменной (
показывает, какая часть (доля) вариации объясняемой переменной обусловлена вариацией объясняющей переменной (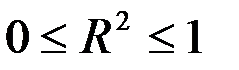 ). Чем ближе
). Чем ближе 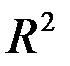 к единице, тем лучше регрессия аппроксимирует эмпирические данные. Если
к единице, тем лучше регрессия аппроксимирует эмпирические данные. Если 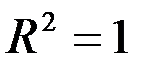 , то между
, то между 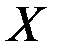 и
и 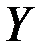 существует линейная функциональная зависимость. Если
существует линейная функциональная зависимость. Если 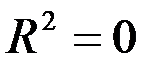 , то объясняемая переменная не зависит от данного набора объясняющих переменных.
, то объясняемая переменная не зависит от данного набора объясняющих переменных. 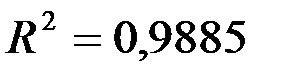 свидетельствует о том, что изменения зависимой переменной
свидетельствует о том, что изменения зависимой переменной 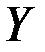 (накопления) в основном можно объяснить изменениями включенных в модель объясняющих переменных – дохода
(накопления) в основном можно объяснить изменениями включенных в модель объясняющих переменных – дохода 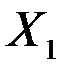 и имущества
и имущества 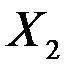 .
.
Нормированный R-квадрат – скорректированный (адаптированный, поправленный(adjusted)) коэффициент детерминации.
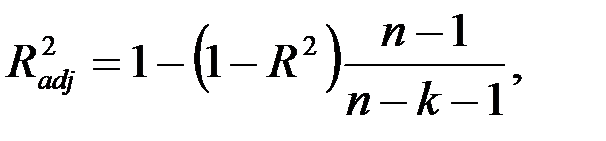
где 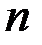 – число наблюдений,
– число наблюдений, 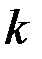 – число объясняющих переменных.
– число объясняющих переменных.
Недостатком коэффициента детерминации 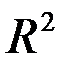 является то, что он увеличивается при добавлении новых объясняющих переменных, хотя это и не обязательно означает улучшение качества регрессионной модели. В этом смысле предпочтительнее использовать
является то, что он увеличивается при добавлении новых объясняющих переменных, хотя это и не обязательно означает улучшение качества регрессионной модели. В этом смысле предпочтительнее использовать 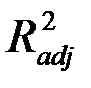 . В отличие от
. В отличие от 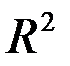 скорректированный коэффициент
скорректированный коэффициент 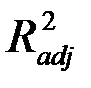 может уменьшаться при введении в модель новых объясняющих переменных, не оказывающих существенное влияние на зависимую переменную.
может уменьшаться при введении в модель новых объясняющих переменных, не оказывающих существенное влияние на зависимую переменную.
Стандартная ошибка регрессии 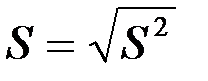 , где
, где 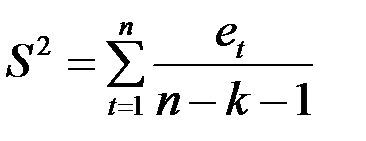 – необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
– необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
Наблюдения – число наблюдений.
Отчет приведен в таблице 1.
Таблица 1а.
| df | SS | MS | F | Значи-мость F | |
| Регрессия | 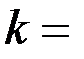 2 2 | 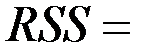 12.02 12.02 | 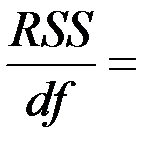 6.01 6.01 | 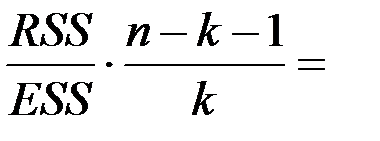 = 42.753 = 42.753 | 0.023 |
| Остаток | 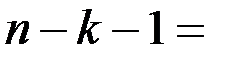 2 2 | 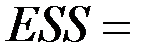 0.28 0.28 | 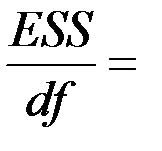 0.14 0.14 | ||
| Итого | 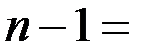 4 4 | 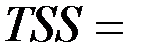 12.30 12.30 |
Таблица 1б.
| Коэффи-циенты | Стандарт-ная ошибка | t-стати-стика | P-Значение | Нижние 95% | Верхние 95% | |
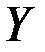 | 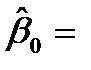 0.279 0.279 | 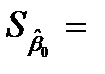 0.894 0.894 | 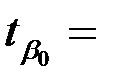 0.312 0.312 | 0.785 | -3.570 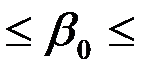 4.127 4.127 | |
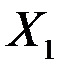 | 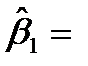 0.123 0.123 | 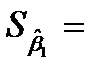 0.018 0.018 | 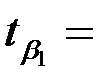 6.692 6.692 | 0.022 | 0.044 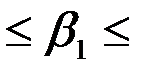 0.202 0.202 | |
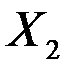 | 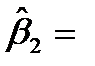 -0.03 -0.03 | 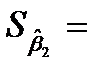 0.007 0.007 | 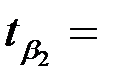 -4.37 -4.37 | 0.050 | -0.059 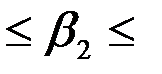 0.000 0.000 |
Таким образом, получена следующая модель:
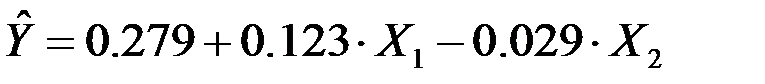
df – degrees of freedom – число степеней свободы связано с числом единиц совокупности 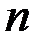 и с числом определяемых по ней констант
и с числом определяемых по ней констант 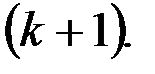 .
.
F и Значимость F позволяют проверить значимость уравнения регрессии, т.е. установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
По эмпирическому значению статистики F проверяется гипотеза равенства нулю одновременно всех коэффициентов модели. Значимость F – теоретическая вероятность того, что при гипотезе равенства нулю одновременно всех коэффициентов модели F -статистика больше эмпирического значения F.
Уравнение регрессии значимо на уровне 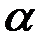 , если
, если 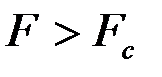 , где
, где 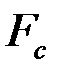 - табличное значение F -критерия Фишера (
- табличное значение F -критерия Фишера (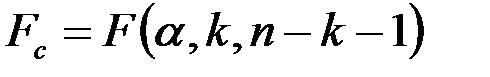 ).
).
На уровне значимости 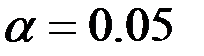 гипотеза
гипотеза 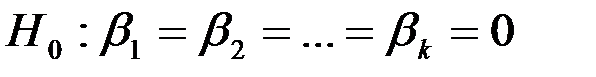 отвергается,
отвергается,
если Значимость 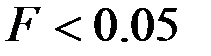 , и принимается, если Значимость
, и принимается, если Значимость 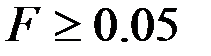 .
.
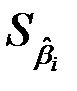 – стандартные ошибки коэффициентов.
– стандартные ошибки коэффициентов.
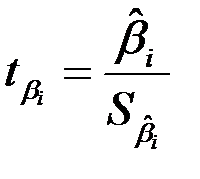 – t -статистика соответствующего коэффициента
– t -статистика соответствующего коэффициента 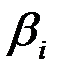 .
.
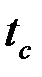 – критическая точка распределения Стьюдента,
– критическая точка распределения Стьюдента, 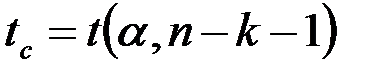 .
.
Если 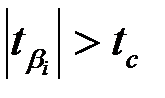 , то коэффициент
, то коэффициент 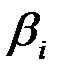 считается статистически значимым.
считается статистически значимым.
Если 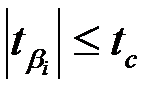 , то коэффициент
, то коэффициент 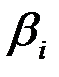 считается статистически незначимым. Это означает, что фактор
считается статистически незначимым. Это означает, что фактор 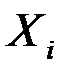 линейно не связан с зависимой переменной
линейно не связан с зависимой переменной 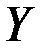 . Его наличие среди объясняющих переменных не оправдано со статистической точки зрения. Поэтому после установления того факта, что коэффициент
. Его наличие среди объясняющих переменных не оправдано со статистической точки зрения. Поэтому после установления того факта, что коэффициент 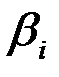 незначим, рекомендуется исключить из уравнения регрессии переменную
незначим, рекомендуется исключить из уравнения регрессии переменную 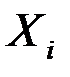 . Это не приведет к существенной потере качества модели, но сделает ее более корректной.
. Это не приведет к существенной потере качества модели, но сделает ее более корректной.
P-Значение – вероятность, позволяющая определить значимость коэффициента регрессии 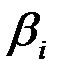 .
.
Для уровня значимости 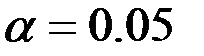 :
:
Если P-Значение 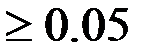 , то коэффициент
, то коэффициент 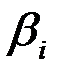 незначим, следовательно, гипотеза
незначим, следовательно, гипотеза 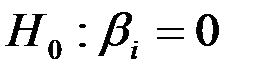 принимается.
принимается.
Если P-Значение 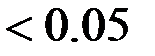 , то коэффициент
, то коэффициент 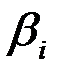 значим, следовательно, гипотеза
значим, следовательно, гипотеза 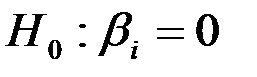 отвергается.
отвергается.
Нижние 95% - Верхние 95% - доверительный интервал для параметра 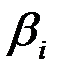 .
.
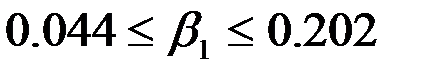 , т.е. с надежностью 0.95 этот коэффициент лежит в данном интервале. Поскольку коэффициент регрессии в эконометрических исследованиях имеют четкую экономическую интерпретацию, то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов, например,
, т.е. с надежностью 0.95 этот коэффициент лежит в данном интервале. Поскольку коэффициент регрессии в эконометрических исследованиях имеют четкую экономическую интерпретацию, то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов, например, 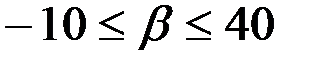 . Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.
. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.
Интерпретация коэффициентов модели: При нулевых значениях «дохода» и «имущества» накопление будет равно 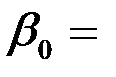 0.279. Так как P -значение этого коэффициента равно 0.785, то он незначимо отличается от нуля.
0.279. Так как P -значение этого коэффициента равно 0.785, то он незначимо отличается от нуля.
То, что коэффициент 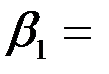 0.123, означает, что при увеличении дохода на 1$ накопления возрастают на 0.123$, а то, что коэффициент
0.123, означает, что при увеличении дохода на 1$ накопления возрастают на 0.123$, а то, что коэффициент 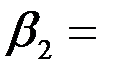 -0.029, означает, что увеличение имущества на 1$ приводит к уменьшению накоплений на 0.029$. Анализ P -значений показывает, что оба коэффициента значимы.
-0.029, означает, что увеличение имущества на 1$ приводит к уменьшению накоплений на 0.029$. Анализ P -значений показывает, что оба коэффициента значимы.
 2015-06-28
2015-06-28 7880
7880
