Радианное измерение углов и дуг

Тригонометрические функции числового аргумента.

В геометрии углом называется фигура, образованная двумя лучами, выходящими из одной точки.

Любой угол можно рассматривать как результат вращения луча в плоскости вокруг начальной точки. Вращая луч вокруг точки О от начального положения OA до конечного положения ОВ, получим угол АОВ (рис. 1).

Понятие об измерении углов известно из геометрии. При измерении углов принимают некоторый определенный угол за единицу измерения и с ее помощью измеряют другие углы.

За единицу измерения можно принять любой угол.

На практике уже более трех тысяч лет за единицу измерения величины угла принята  часть полного оборота, которую называют градусом.

  Рис. 1.

В технике за единицу измерения углов принимают полный оборот.

В мореплавании за единицу измерения углов принят румб, равный 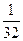 части полного оборота.

В артиллерии за единицу измерения углов принята  часть полного оборота, которую называют большим делением угломера (0,01 часть большого деления угло­мера называют малым делением угломера).

В связи с развитием техники появилась потребность измерять круговые движения (т. е. повороты на сколь угодно большие углы и различные колебательные процессы, связанные с круговым движением). Появилась потребность в новой, универсальной единице измерения дуг и углов. Такой единицей оказалась радианная (радиусная) мера угла, она появилась в трудах Ньютона (1643—1727) и Лейбница (1646—1716) и вошла в науку благодаря трудам академика Петербургской академии наук Леонарда Эйлера (1707—1783).

Вы хорошо знакомы с числовой осью, т. е. прямой, на которой отмечена начальная точка О, единица масштаба ОЕ и положительное направление. При помощи числовой оси устанавливается взаимно однозначное соответствие между множеством действительных чисел и множеством точек прямой. Каждому действительному числу z ставится в соответствие определенная точка М, которая является концом отрезка ОМ длины | z |. Отрезок ОМ откладывается в положительном направлении, если z > 0, и в отрицательном, если z < 0. Точка О соответствует числу z = 0. Действительное число z называется координатой точки М и записывается M (z).

Пусть дана некоторая единичная окружность, т.е. окружность с центром в некоторой точке О и с радиусом, равным единице масштаба. Выберем на этой окружности некоторую точку А (рис.2).

По аналогии с прямой каждому числу 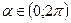 поставим в соответствие точку М_α данной единичной окружности такую, что длина дуги АМ_α равна α, причем дуга АМ_α откладывается от точки А против часовой стрелки. Числу 0 и числу 2 π поставим в соответствие точку А. Таким образом, между точками единичной окружности и числами промежутка [0; 2 π [ установлена взаимно однозначное соответствие.

   Рис. 2.

Число α называется радианной мерой дуги АМ_α и соответственно угла АОМ_α.

Из формулы для вычисления длины дуги окружности следует формула, связывающая радианную и градусную меры угла. Действительно, если α – длина дуги единичной окружности, градусная мера которой равна β, то .

Таким образом, дуга в 1 радиан содержит  градусов: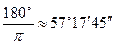

Дуга в 1° содержит  радиан: .

Пример: Выразить в радианной мере углы 120; 320.

Ответ: Так как , то , .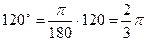

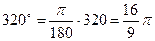Для перевода меры угла из градусной в радианную и обратно существуют таблицы (см., например, В. М. Брадис, Четырехзначные математические таблицы).

Приведем таблицу для углов и дуг, которые встре­чаются часто.

 

Градусы	360°	180°	90°	60°	45°	30°	18°	15°	10°	1°	β °
Радианы	2 π	π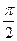

 

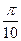
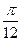
Снова рассмотрим единичную окружность с выбран­ной точкой А (рис. 2).

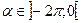Каждому числу  поставим в соответст­вие точку М_α данной единичной окружности такую, что длина дуги АМ_α равна | α | и дуга АМ_α откладывается от точки А по часовой стрелке (рис. 3). Числу - 2 π поставим в соответствие точку А.

Произвольное число α представим следующим образом: , где k — некоторое целое число, а . Заметим, что для любого α такое представление возможно. Теперь числу α поставим в соответствие ту же точку, что и числу α ₀, т. е. точки М_α и  совпадают.

       Рис. 3.

 

Таким образом, выше построено соответствие между действительными числами и точками единичной окружности. Из самого построения этого соответствия следует, что точки , ,  совпадают.

О точке М_α говорят, что она получается из точки А поворотом на | α | радиан против часовой стрелки, если α > 0, и по часовой стрелке, если α < 0. Вращение против часовой стрелки иногда называют вращением в положительном направлении, а вращение по часовой стрелке — вращением в отрицательном направлении.