Раздел 2
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
· Дискретная случайная величина
· Непрерывная случайная величина
· Нормальный закон распределения
· Предельные теоремы теории вероятностей
Одним из основных понятий теории вероятностей является, наряду со случайным событием, понятие случайной величины.
• Случайная величина — это переменная, которая в результате испытания принимает одно из своих возможных значений, причем заранее не известно, какое именно, так как оно зависит от случая.
Связь случайной величины и случайного события заключается в том, что принятие случайной величиной некоторого числового значения из набора возможных (т. е. выполнение равенства  )[1] есть случайное событие, характеризующееся вероятностью
)[1] есть случайное событие, характеризующееся вероятностью  .
.
Примеры случайных величин:
• число очков, выпавших на верхней грани игрального кубика;
• число студентов, пришедших на лекцию;
• расстояние от центра мишени до точки попадания при выстреле;
• сумма выплаты по очередному страховому случаю и т. п.
Для определения случайной величины необходимо задать ее закон распределения.
• Закон распределения — соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями, с которыми случайная величина принимает эти значения.
Для практического применения не всегда необходимо иметь полное представление о случайной величине, достаточно знать некоторые ее числовые характеристики, дающие суммарное представление о случайной величине, к которым, прежде всего, относятся математическое ожидание и дисперсия.
• Математическое ожидание М(Х) — это число, характеризующее среднее значение случайной величины X.
Свойства математического ожидания:
· математическое ожидание постоянной величины С=const равно этой величине:
М(С)=С;
· математическое ожидание произведения постоянной величины С=const и случайной величины X равно произведению этой константы на математическое ожидание случайной величины (константу можно вынести за знак математического ожидания):
М(С*Х)=С*М(Х);
· математическое ожидание алгебраической суммы п случайных величин 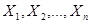 равно алгебраической сумме математических ожиданий этих случайных величин:
равно алгебраической сумме математических ожиданий этих случайных величин:
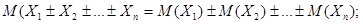
· математическое ожидание произведения n независимых случайных величин 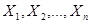 равно произведению математических ожиданий этих случайных величин:
равно произведению математических ожиданий этих случайных величин:

· математическое ожидание алгебраической суммы случайной величины Xи постоянной величины С=const равно алгебраической сумме этой константы и математического ожидания случайной величины:
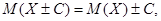
в частности, 
· математическое ожидание среднего арифметического значения n одинаково распределенных (имеющих одинаковые законы распределения) взаимно независимых случайных величин 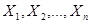 равно математическому ожиданию этих величин:
равно математическому ожиданию этих величин:

• Дисперсия характеризует разброс или рассеяние значений случайной величины около ее математического ожидания.
• Дисперсия — это математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

Свойства дисперсии:
· дисперсия постоянной величины C=const равна нулю:
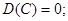
· дисперсия произведения постоянной величины С=const и случайной величины X равна произведению квадрата этой константы на дисперсию случайной величины (константу можно вынести за знак дисперсии, возведя ее в квадрат):
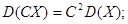
· дисперсия алгебраической суммы или разности n независимых случайных величин 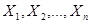 равна сумме дисперсий этих случайных величин:
равна сумме дисперсий этих случайных величин:
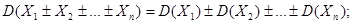
· дисперсия алгебраической суммы случайной величины Х и постоянной величины С=const равна дисперсии случайной величины:
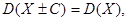
в частности, 
· дисперсии суммы и среднего арифметического значения n одинаково распределенных (имеющих одинаковые законы распределения) взаимно независимых случайных величин 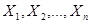 , дисперсия каждой из которых равна
, дисперсия каждой из которых равна 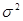 , равны
, равны 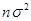
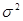 и соответственно:
и соответственно:


· Формула упрощенного вычисления дисперсии имеет вид:
 (1.32)
(1.32)
Действительно,

В зависимости от характера области возможных значений выделяют два типа случайных величин: дискретные и непрерывные.
Глава 5. ДИСКРЕТНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА
· Дискретная случайная величина — случайная величина, которая принимает конечное или бесконечное, но счетное число отдельных изолированных значений (т. е. их можно перенумеровать натуральными числами).
Понятие дискретной случайной величины тесным образом связано с понятием случайного события, являясь в некотором смысле его обобщением. При определении дискретной случайной величины первичным понятием также является испытание, результат которого характеризуется не альтернативным исходом (появится событие или нет), а некоторым числом (числом появления события в серии независимых испытаний; числом очков, выбиваемых стрелком; числом вкладчиков, посетивших отделение банка за определенный период времени, и т. д.).
Для дискретной случайной величины простейшей формой задания закона распределения является ряд распределения, представляющий собой таблицу, в верхней строке которой указаны возможные значения  , дискретной случайной величины Х, а в нижней — соответственно вероятности
, дискретной случайной величины Х, а в нижней — соответственно вероятности  , того, что X примет значение
, того, что X примет значение  :
:

| 
| 
| … | 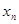
|
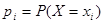
| 
| 
| … | 
|
При построении ряда распределения необходимо помнить, что:
1.  , по свойству вероятности
, по свойству вероятности  ;
;
2.  , так как события
, так как события  ,
,  , …,
, …,  составляют полную группу попарно несовместных событий.
составляют полную группу попарно несовместных событий.
• Графическое представление ряда распределения называется многоугольником (полигоном) распределения.
.







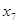 х
х
Рис. 7. Полигон распределения дискретной случайной величины Х
Для его построения возможные значения  дискретной случайной величины Х откладываются по оси абсцисс, а соответствующие вероятности
дискретной случайной величины Х откладываются по оси абсцисс, а соответствующие вероятности 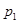 — по оси ординат; точки с координатами (
— по оси ординат; точки с координатами ( ;
;  ) соединяются отрезками.
) соединяются отрезками.
 2020-06-08
2020-06-08 73
73







